已知n是不小于3的正整數,
an=| n |
 |
| k=1 |
k,
bn=| n |
 |
| k=1 |
k2.
(1)求a
n,b
n;
(2)設
cn=,求證:
| n |
 |
| k=1 |
(ckck+1)<2.
分析:(1)由于a
n,b
n是以和式出現,而且與組合數有關,借助于kC
nk=nC
n-1k-1,可進行轉化,從而求出數列的通項公式;
(2)由(1)知
cn==,∴
ckck+1=4(-),從而利用裂項求和法求和,故可證.
解答:解:(1)
an=| n |
 |
| k=1 |
k=+2+…+n,
因為kC
nk=nC
n-1k-1,所以a
n=nC
n-10+nC
n-11+…+nC
n-1n-1=n(C
n-10+C
n-11+…+C
n-1n-1)=n•2
n-1.…3分
因為k
2C
nk=k•kC
nk=k•nC
n-1k-1,而kC
n-1k-1=(k-1)C
n-1k-1+C
n-1k-1=(n-1)C
n-2k-2+C
n-1k-1(k≥2),
所以,
bn=| n |
 |
| k=1 |
k2=n+| n |
 |
| k=2 |
[n(n-1)+n]=n+n(n-1)| n |
 |
| k=2 |
+n| n |
 |
| k=2 |
=n(n-1)•2
n-2+n•2
n-1=n(n+1)•2
n-2.
(2)
cn===,
所以
| n |
 |
| k=1 |
(ckck+1)=4| n |
 |
| k=1 |
(-)=4(-)<2.
點評:本題主要考查數列通項的求解及裂項求和法,同時考查了組合數的性質,有一定的綜合性.
練習冊系列答案
相關習題
科目:高中數學
來源:2012年江蘇省南京市蘇州市梁豐高級中學高考數學一模試卷(解析版)
題型:解答題
已知n是不小于3的正整數,
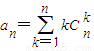
,
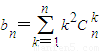
.
(1)求a
n,b
n;
(2)設
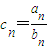
,求證:
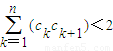
.
查看答案和解析>>
科目:高中數學
來源:2011年江蘇省南通市啟東中學高三數學考前輔導材料(1)(解析版)
題型:解答題
已知n是不小于3的正整數,

,

.
(1)求a
n,b
n;
(2)設

,求證:

.
查看答案和解析>>
科目:高中數學
來源:2011年江蘇省高考數學預測試卷(2)(解析版)
題型:解答題
已知n是不小于3的正整數,
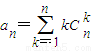
,
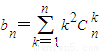
.
(1)求a
n,b
n;
(2)設
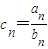
,求證:
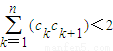
.
查看答案和解析>>
科目:高中數學
來源:2010年江蘇省南通市海安縣高級中學高考數學押題卷(解析版)
題型:解答題
已知n是不小于3的正整數,
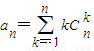
,
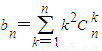
.
(1)求a
n,b
n;
(2)設
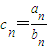
,求證:

.
查看答案和解析>>













 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案