
分析 利用換元法,轉化為二次函數問題,利用二次函數性質即可求最大值.
解答 解:函數y=sinxcosx+sinx+cosx.
令sinx+cosx=t,
由于sinx+cosx=$\sqrt{2}$sin(x+$\frac{π}{4}$)=t,
∴$-\sqrt{2}≤$t$≤\sqrt{2}$
則sinxcosx=$\frac{{t}^{2}-1}{2}$.
那么:函數y 轉化為g(t)=$\frac{1}{2}{t}^{2}+t-\frac{1}{2}$,($-\sqrt{2}≤$t$≤\sqrt{2}$)
可知g(t)開口向上,對稱軸x=$-\frac{1}{4}$,
∴當$-\sqrt{2}≤$t$≤-\frac{1}{4}$上時,函數g(t)是單調遞減.
∴當$-\frac{1}{4}≤t≤\sqrt{2}$上時,函數g(t)是單調遞增.
∴g($\sqrt{2}$)max=$\frac{1}{2}+\sqrt{2}$
故答案為:$\frac{1}{2}+\sqrt{2}$.
點評 本題考查了三角函數性質及化解能力,轉化思想和換元法.利用了二次函數的性質.屬于基礎題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | ln 2+1 | C. | ln 2-1 | D. | ln 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{4}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{8}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
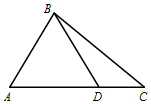 在△ABC中(圖),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7},\overrightarrow{AD}=2\overrightarrow{DC}$.
在△ABC中(圖),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7},\overrightarrow{AD}=2\overrightarrow{DC}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,長方體ABCD-A1B1C1D1中,點M在棱BB1上,兩條直線MA,MC與平面ABCD所成角均為θ,AC與BD交于點O.
如圖,長方體ABCD-A1B1C1D1中,點M在棱BB1上,兩條直線MA,MC與平面ABCD所成角均為θ,AC與BD交于點O.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
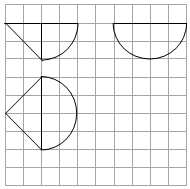 某組合體的三視圖如圖所示,圖中網格每個小正方形的邊長為1,曲線均為圓弧的一部分,則該幾何體的體積為( )
某組合體的三視圖如圖所示,圖中網格每個小正方形的邊長為1,曲線均為圓弧的一部分,則該幾何體的體積為( )| A. | $\frac{28}{3}π$ | B. | 4π | C. | $\frac{10}{3}π$ | D. | $\frac{2}{3}+\frac{8}{3}π$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com