
【題目】在三棱錐DABC中,ADDC,ACCB,AB=2AD=2DC=2,且平面ABD平面BCD,E為AC的中點.
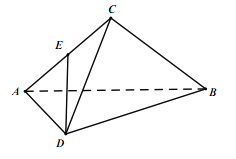
(I)證明:ADBC;
(II)求直線 DE 與平面ABD所成的角的正弦值.
科目:高中數學 來源: 題型:
【題目】如圖,在中國象棋規則下,點A處的“兵”可通過某條路徑到達點B(兵在過河前每步只能走到其前方相鄰的交叉點處,過河之后每步則可走到前方、左方、右方相鄰的交叉點處,但不能后退,“河”是指圖棋盤中第5、6條橫線之間的部分).在兵的行進過程中,若棋盤的每個交叉點均不被兵重復走到,則稱此路徑為“無重復路徑”.那么,不同的無重復路徑的條數為__________。
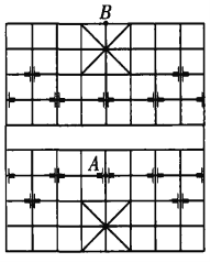
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐P﹣ABC中,E,F分別為AC,BC的中點.
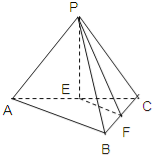
(1)求證:EF∥平面PAB;
(2)若平面PAC⊥平面ABC,且PA=PC,∠ABC=90°,求證:平面PEF⊥平面PBC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】雙曲線![]() 的左焦點為
的左焦點為![]() ,點A的坐標為(0,1),點P為雙曲線右支上的動點,且△APF1周長的最小值為6,則雙曲線的離心率為( )
,點A的坐標為(0,1),點P為雙曲線右支上的動點,且△APF1周長的最小值為6,則雙曲線的離心率為( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數![]() .
.
(1)若函數在區間![]() 上存在零點,求實數p的取值范圍;
上存在零點,求實數p的取值范圍;
(2)問是否存在常數![]() ,使得當
,使得當![]() 時,
時,![]() 的值域為區間D,且D的長度為
的值域為區間D,且D的長度為![]() .
.
(注:區間![]()
![]() 的長度為
的長度為![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是橢圓
是橢圓![]() 上任一點,點
上任一點,點![]() 到直線
到直線![]() :
:![]() 的距離為
的距離為![]() ,到點
,到點![]() 的距離為
的距離為![]() ,且
,且![]() ,若直線
,若直線![]() 與橢圓
與橢圓![]() 交于不同兩點
交于不同兩點![]() 、
、![]() (
(![]() 、
、![]() 都在
都在![]() 軸上方),且
軸上方),且![]() .
.
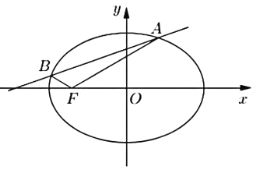
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)當![]() 為橢圓與
為橢圓與![]() 軸正半軸的交點時,求直線
軸正半軸的交點時,求直線![]() 的方程;
的方程;
(3)對于動直線![]() ,是否存在一個定點,無論
,是否存在一個定點,無論![]() 如何變化,直線
如何變化,直線![]() 總經過此定點?若存在,求出定點的坐標,若不存在,請說明理由.
總經過此定點?若存在,求出定點的坐標,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com