
【題目】已知二次函數![]() .
.
(1)若函數在區間![]() 上存在零點,求實數p的取值范圍;
上存在零點,求實數p的取值范圍;
(2)問是否存在常數![]() ,使得當
,使得當![]() 時,
時,![]() 的值域為區間D,且D的長度為
的值域為區間D,且D的長度為![]() .
.
(注:區間![]()
![]() 的長度為
的長度為![]() ).
).
【答案】(1)–20≤p≤12;(2)存在常數q= 8或q= 9,當x∈[q,10]時,![]() 的值域為區間
的值域為區間![]() ,且
,且![]() 的長度為12–q.
的長度為12–q.
【解析】
(1)利用零點存在性定理列出關于q的不等式,然后再利用不等式知識求解即可;(2)先利用單調性求出函數的值域,再利用區間長度列出關于q的方程,求解即可。
解:(1)∵二次函數f(x)=x2– 16x+p+ 3的對稱軸是![]() ,∴函數
,∴函數![]() 在區間
在區間![]() 上單調遞減,則函數
上單調遞減,則函數![]() 在區間
在區間![]() 上存在零點須滿足
上存在零點須滿足![]() . ……………2分
. ……………2分
即(1 + 16 +p+ 3)(1 – 16 +p+ 3)≤0, 解得–20≤p≤12. …………………4分
⑵ 當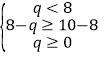 時,即0≤q≤6時,
時,即0≤q≤6時,
![]() 的值域為:[f(8),f(q)],即[p–61,q2–16q+p+ 3].
的值域為:[f(8),f(q)],即[p–61,q2–16q+p+ 3].
∴區間長度為q2– 16q+p+ 3 – (p– 61) =q2– 16q+ 64 =" 12" –q.
∴q2– 15q+ 52 =" 0" ∴![]() ,經檢驗
,經檢驗![]() 不合題意,舍去.……6分
不合題意,舍去.……6分
當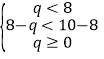 時,即6≤q<8時,
時,即6≤q<8時,![]() 的值域為:
的值域為:![]() ,即[p– 61,p– 57]
,即[p– 61,p– 57]
∴區間長度為p– 57 – (p– 61) =" 4" =" 12" –q∴q= 8.經檢驗q= 8不合題意,舍去. …8分
當q≥8時,![]() 的值域為:[f(q),f(10)],即 [q2– 16q+p+3,p– 57].
的值域為:[f(q),f(10)],即 [q2– 16q+p+3,p– 57].
∴區間長度為p– 57 –(q2– 16q+p+ 3) = –q2– 16q– 60 =" 12" –q,
∴q2– 17q+ 72 =" 0" , ∴q= 8或q= 9.經檢驗q= 8或q= 9滿足題意.
所以存在常數q= 8或q= 9,當x∈[q,10]時,![]() 的值域為區間
的值域為區間![]() ,且
,且![]() 的長度為12–q. ………………………10分
的長度為12–q. ………………………10分


科目:高中數學 來源: 題型:
【題目】某班制定了數學學習方案:星期一和星期日分別解決![]() 個數學問題,且從星期二開始,每天所解決問題的個數與前一天相比,要么“多一個”要么“持平”要么“少一個”,則在一周中每天所解決問題個數的不同方案共有( )
個數學問題,且從星期二開始,每天所解決問題的個數與前一天相比,要么“多一個”要么“持平”要么“少一個”,則在一周中每天所解決問題個數的不同方案共有( )
A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在邊長為60 cm的正方形鐵片的四角上切去相等的正方形,再把它沿虛線折起,做成一個無蓋的長方體箱子,箱底的邊長是多少時,箱子的容積最大?最大容積是多少?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐DABC中,ADDC,ACCB,AB=2AD=2DC=2,且平面ABD平面BCD,E為AC的中點.
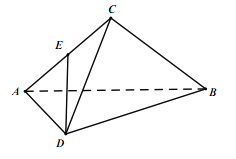
(I)證明:ADBC;
(II)求直線 DE 與平面ABD所成的角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①,已知矩形ABCD滿足AB=5,![]() ,沿平行于AD的線段EF向上翻折(點E在線段AB上運動,點F在線段CD上運動),得到如圖②所示的三棱柱
,沿平行于AD的線段EF向上翻折(點E在線段AB上運動,點F在線段CD上運動),得到如圖②所示的三棱柱![]() .
.
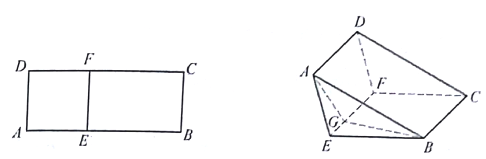
⑴若圖②中△ABG是直角三角形,這里G是線段EF上的點,試求線段EG的長度x的取值范圍;
⑵若⑴中EG的長度為取值范圍內的最大整數,且線段AB的長度取得最小值,求二面角![]() 的值;
的值;
⑶在⑴與⑵的條件都滿足的情況下,求三棱錐A-BFG的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC-A1B1C1中,側面AA1C1C是矩形,平面ABC⊥平面AA1C1C,AB=2,AC=1,![]() ,
,![]() .
.
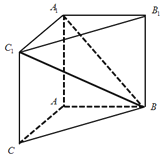
(1)求證:AA1⊥平面ABC;
(2)在線段BC1上是否存在一點D,使得AD⊥A1B?若存在求出![]() 的值,若不存在請說明理由.
的值,若不存在請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌經銷商在一廣場隨機采訪男性和女性用戶各50名,其中每天玩微信超過6小時的用戶列為“微信控”,否則稱其為“非微信控”,調查結果如下:
微信控 | 非微信控 | 合計 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合計 | 56 | 44 | 100 |
(1)根據以上數據,能否有95%的把握認為“微信控”與“性別”有關?
(2)現從調查的女性用戶中按分層抽樣的方法選出5人,求所抽取的5人中“微信控”和“非微信控”的人數;
(3)從(2)中抽取的5位女性中,再隨機抽取3人贈送禮品,試求抽取3人中恰有2人位“微信控”的概率.
參考公式: 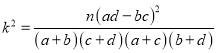 ,其中
,其中![]() .
.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系(
軸正半軸為極軸,建立極坐標系(![]() ),點
),點![]() 為曲線
為曲線![]() 上的動點,點
上的動點,點![]() 在線段
在線段![]() 的延長線上,且滿足
的延長線上,且滿足![]() ,點
,點![]() 的軌跡為
的軌跡為![]() 。
。
(Ⅰ)求![]() 的極坐標方程;
的極坐標方程;
(Ⅱ)設點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 面積的最小值。
面積的最小值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com