
【題目】如圖,在四棱錐P﹣ABCD中,PA⊥面ABCD,AB∥CD,CD⊥AD,AD=CD=2AB=2,E,F分別為PC,CD的中點 
(1)求證:平面ABE⊥平面BEF
(2)設PA=a,若平面EBD與平面ABCD所成銳二面角θ∈[ ![]() ,
, ![]() ],求a的取值范圍.
],求a的取值范圍.
【答案】
(1)證明:以A為原點,以AB,AD,AP為坐標軸建立空間直角坐標系,設PA=a,
則A(0,0,0),B(1,0,0),F(1,2,0,),E(1,1, ![]() ),
),
∴ ![]() =(1,0,0),
=(1,0,0), ![]() =(0,1,
=(0,1, ![]() ),
), ![]() =(0,2,0),
=(0,2,0),
∴ ![]() =0,
=0, ![]() =0,
=0,
∴AB⊥BE,AB⊥BF,又BE∩BF=B,
AB⊥平面BEF,又AB平面ABE,
∴平面ABE⊥平面BEF
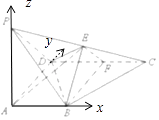
(2)解:由(1)知 ![]() =(﹣1,2,0),
=(﹣1,2,0), ![]() =(0,1,
=(0,1, ![]() ),
),
設平面BDE的法向量為 ![]() =(x,y,z),則
=(x,y,z),則 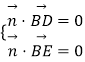 ,
,
∴ 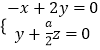 ,令z=1得
,令z=1得 ![]() =(﹣a,﹣
=(﹣a,﹣ ![]() ,1),
,1),
∵PA⊥平面ABCD,∴ ![]() =(0,0,1)是平面ABCD的一個法向量,
=(0,0,1)是平面ABCD的一個法向量,
∴cos< ![]() >=
>= ![]() =
= ![]() ,
,
∵平面EBD與平面ABCD所成銳二面角θ∈[ ![]() ,
, ![]() ],
],
∴ ![]() ≤
≤ ![]() ≤
≤ ![]() ,
,
解得: ![]() ≤a≤
≤a≤ ![]() .
.
【解析】(1)建立坐標系,設PA=a,求出各向量的坐標,利用數量積證明AB⊥BF,AB⊥BE,故而AB⊥平面BEF,于是平面ABE⊥平面BEF;(2)求出兩平面的法向量,計算法向量的夾角,根據二面角的范圍列不等式組解出a的范圍.
【考點精析】關于本題考查的平面與平面垂直的判定,需要了解一個平面過另一個平面的垂線,則這兩個平面垂直才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 在區間
在區間![]() 上有最大值4 和最小值1,設
上有最大值4 和最小值1,設![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在區間
在區間![]() 上有解,求實數
上有解,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() 有三個不同的實數解,求實數
有三個不同的實數解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正△ABC三個頂點都在半徑為2的球面上,球心O到平面ABC的距離為1,點E是線段AB的中點,過點E作球O的截面,則截面面積的最小值是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】參與舒城中學數學選修課的同學對某公司的一種產品銷量與價格進行了統計,得到如下數據和散點圖.
定價x(元/千克) | 10 | 20 | 30 | 40 | 50 | 60 |
年銷量y(千克) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=2 ln y | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |

參考數據:
![]() ,
,
![]() .
.
(1)根據散點圖判斷y與x,z與x哪一對具有較強的線性相關性(給出判斷即可,不必說明理由)?
(2)根據(1)的判斷結果及數據,建立y關于x的回歸方程(方程中的系數均保留兩位有效數字).
(3)當定價為150元/千克時,試估計年銷量.
附:對于一組數據(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回歸直線![]() x+
x+![]() 的斜率和截距的最
的斜率和截距的最
小二乘估計分別為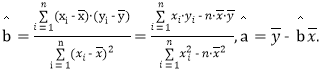
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】德國著名數學家狄利克雷在數學領域成就顯著,以其名命名的函數f(x)= ![]() ,稱為狄利克雷函數,則關于函數f(x)有以下四個命題: ①f(f(x))=1;
,稱為狄利克雷函數,則關于函數f(x)有以下四個命題: ①f(f(x))=1;
②函數f(x)是偶函數;
③任意一個非零有理數T,f(x+T)=f(x)對任意x∈R恒成立;
④存在三個點A(x1 , f(x1)),B(x2 , f(x2)),C(x3 , f(x3)),使得△ABC為等邊三角形.
其中真命題的個數是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x﹣4|,g(x)=|2x+1|.
(1)解不等式f(x)<g(x);
(2)若2f(x)+g(x)>ax對任意的實數x恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓的兩焦點為![]() ,
,![]() ,離心率
,離心率![]() .
.
(1)求此橢圓的方程;
(2)設直線![]() :
:![]() ,若
,若![]() 與此橢圓相交于
與此橢圓相交于![]() ,
,![]() 兩點,且
兩點,且![]() 等于橢圓的短軸長,求
等于橢圓的短軸長,求![]() 的值;
的值;
(3)以此橢圓的上頂點![]() 為直角頂點作橢圓的內接等腰直角三角形
為直角頂點作橢圓的內接等腰直角三角形![]() ,這樣的直角三角形是否存在?若存在,請說明有幾個;若不存在,請說明理由.
,這樣的直角三角形是否存在?若存在,請說明有幾個;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=xln(ax+1)(a≠0).
(Ⅰ)討論f(x)的單調性;
(Ⅱ)若a>0且滿足:對x1 , x2∈[﹣1,1],都有|f(x1)﹣f(x2)|≤ln3﹣ln2,試比較ea﹣1與 ![]() 的大小,并證明.
的大小,并證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com