已知:如圖,在梯形ABCD中,AD∥BC∥EF,E是AB的中點,EF交BD于G,交AC于H. 若AD=5,BC=7,則GH=________.
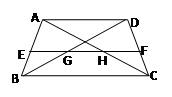
分析:根據(jù)梯形中位線的性質(zhì),計算出EF的長,再根據(jù)三角形中位線的性質(zhì),求出EG和HF的長,從而計算出GH的長.
解:∵EF是梯形ABCD的中位線,
∴E、GH、F分別為AB、BD、AC、DC的中點,
又∵AD=5,BC=7,
∴EF=(5+7)÷2=6,EG=HF=6÷2=3,
∴GH=EF-EG-HF=7-3-3=1.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
在
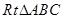
中,
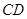
、
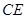
分別是斜邊
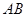
上的高和中線,是該圖中共有
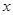
個三角形與
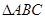
相似,則
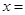
( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
(二)選做題(14-15題,考生只能從中選做一題)
14.(坐標

系與參數(shù)方程選做題)圓C的極坐標方程
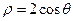
化為直角坐標方程為
,該圓的面積為
.
15.(幾何證明選講選做題)如圖,圓
O的割線
PBA過圓心
O,弦
CD交
PA于點
F,且△
COF∽△
PDF,
PB =
OA = 2,則
PF =
。
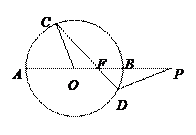
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
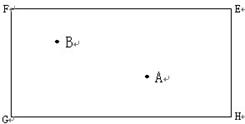
如圖:四邊形
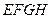
是一個長方形

臺球桌面,有白、黑兩球分別位于
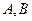
兩點的位置上.試問,怎樣撞擊白球
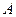
,才能使

白球
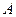
先碰撞臺邊
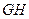
,再碰撞
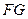
,經(jīng)兩次反彈后再擊中黑球
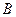
?
(將白球
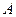
移動路線畫在圖上,不能說明問題的不予計分)
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知直線
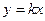
與圓
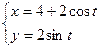
(
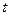
為參數(shù))相切,則直線的傾斜角為
A
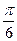
B
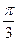

C
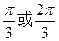
D
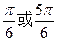
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
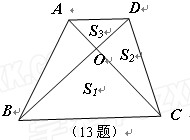
如圖,在梯形ABCD中,AD//BC,AC、BD相交于O,記△BCO、△CDO、△ADO的面積分別為S1、S2、S3,則
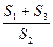
的取值范圍是 .
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
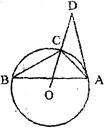
(幾何證明選講)如圖,已知△ABC內(nèi)接于圓O,點D在OC
的延長線上,AD是⊙0的切線,若∠B=30°,AC=2,則OD的長為
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
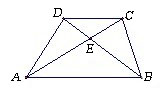
(幾何證明選講選做題) 如圖,梯形
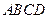
,
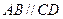
,
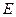
是對角線
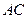
和
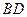
的交點,
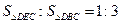
,則
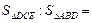
。
查看答案和解析>>

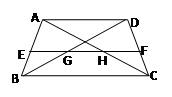
 系與參數(shù)方程選做題)圓C的極坐標方程
系與參數(shù)方程選做題)圓C的極坐標方程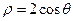 化為直角坐標方程為 ,該圓的面積為 .
化為直角坐標方程為 ,該圓的面積為 .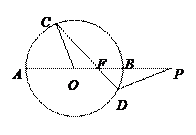
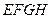 是一個長方形
是一個長方形 臺球桌面,有白、黑兩球分別位于
臺球桌面,有白、黑兩球分別位于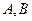 兩點的位置上.試問,怎樣撞擊白球
兩點的位置上.試問,怎樣撞擊白球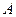 ,才能使
,才能使 白球
白球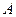 先碰撞臺邊
先碰撞臺邊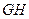 ,再碰撞
,再碰撞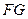 ,經(jīng)兩次反彈后再擊中黑球
,經(jīng)兩次反彈后再擊中黑球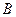 ?
?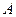 移動路線畫在圖上,不能說明問題的不予計分)
移動路線畫在圖上,不能說明問題的不予計分)
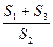 的取值范圍是 .
的取值范圍是 .
