滿足(t,4t)(t<0)的任一組解均可
分析:由f(-2)=2a-
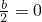
可得b=4a,從而可得
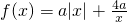
=
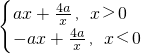
,由函數(shù)的定義域為(-∞,0)(0,+∞),當a>0時,函數(shù)在(2,+∞)單調(diào)遞增,在(-∞,0),(0,2)單調(diào)遞減,當a<0時,函數(shù)在(0,+∞)在(0,2)單調(diào)遞增,在(-∞,0)單調(diào)遞減,當a=0時,函數(shù)f(x)=0不具有單調(diào)性,從而可得
解答:由f(-2)=2a-
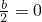
可得,b=4a
∴
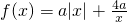
=
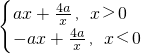
∴函數(shù)的定義域為(-∞,0)(0,+∞)
∵f(x)有兩個單調(diào)遞增區(qū)間
當a>0時,函數(shù)在(2,+∞)單調(diào)遞增,在(-∞,0),(0,2)單調(diào)遞減,不符合題意
當a<0時,函數(shù)在(0,+∞)在(0,2)單調(diào)遞增,在(-∞,0)單調(diào)遞減
當a=0時,函數(shù)f(x)=0不具有單調(diào)性
故滿足條件的a<0
故答案為:(t,4t)(t<0)
點評:本題主要考查了形如f(x)=ax+

的單調(diào)性與參數(shù)a的取值范圍的關系,解題的關鍵是要靈活利用基本初等函數(shù)的單調(diào)行.

 (a,b為常數(shù)),且①f(-2)=0;②f(x)有兩個單調(diào)遞增區(qū)間,則同時滿足上述條件的一個有序數(shù)對(a,b)為________.
(a,b為常數(shù)),且①f(-2)=0;②f(x)有兩個單調(diào)遞增區(qū)間,則同時滿足上述條件的一個有序數(shù)對(a,b)為________.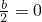 可得b=4a,從而可得
可得b=4a,從而可得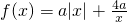 =
=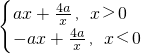 ,由函數(shù)的定義域為(-∞,0)(0,+∞),當a>0時,函數(shù)在(2,+∞)單調(diào)遞增,在(-∞,0),(0,2)單調(diào)遞減,當a<0時,函數(shù)在(0,+∞)在(0,2)單調(diào)遞增,在(-∞,0)單調(diào)遞減,當a=0時,函數(shù)f(x)=0不具有單調(diào)性,從而可得
,由函數(shù)的定義域為(-∞,0)(0,+∞),當a>0時,函數(shù)在(2,+∞)單調(diào)遞增,在(-∞,0),(0,2)單調(diào)遞減,當a<0時,函數(shù)在(0,+∞)在(0,2)單調(diào)遞增,在(-∞,0)單調(diào)遞減,當a=0時,函數(shù)f(x)=0不具有單調(diào)性,從而可得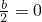 可得,b=4a
可得,b=4a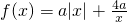 =
=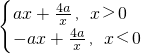
 的單調(diào)性與參數(shù)a的取值范圍的關系,解題的關鍵是要靈活利用基本初等函數(shù)的單調(diào)行.
的單調(diào)性與參數(shù)a的取值范圍的關系,解題的關鍵是要靈活利用基本初等函數(shù)的單調(diào)行. 

 ABC考王全優(yōu)卷系列答案
ABC考王全優(yōu)卷系列答案