分析:(1)取BC中點E,連接B1E,證明BD⊥平面AEB1,得BD⊥AB1,由直線與平面垂直的判定定理,可得所證結論.
(2)連接B1D,則三棱錐B-A1B1D的體積可以通過求三棱錐A1-B1DB的體積得到.
解答:(1)證明:由正三棱柱ABC-A
1B
1C
1的所有棱長都相等可知:AB
1⊥A
1B
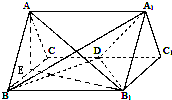
如圖,取BC的中點E,連接B
1E,則Rt△BCD≌Rt△B
1BE
∴∠BB
1E=∠CBD
∴∠CBD+∠BEB
1=∠BB
1E+∠BEB
1=90°
∴BD⊥B
1E
由平面ABC⊥平面BCC
1B
1,平面ABC∩平面BCC
1B
1=BC,且AE⊥BC得,AE⊥平面BCC
1B
1∴AE⊥BD
∵B
1E?平面AEB
1,AE?平面AEB
1,AE∩B
1E=E
∴BD⊥平面AEB
1∴BD⊥AB
1∵A
1B?平面A
1BD,BD?平面A
1BD,A
1B∩BD=B
∴AB
1⊥平面A
1BD
(2)解:連接B
1D,由AA
1∥平面BCC
1B
1所以點A
1到平面BCC
1B
1的距離,等于AE=
==S△BDB1=S正方形BCC1B1=×2×2=2
∴
VB-A1B1D=VA1-BDB1=
×S△BDB1×AE=
×2×=故三棱錐B-A
1B
1D的體積為
.
點評:本題主要考查了線面垂直的判定定理、幾何體體積的求法,解題過程中要注意各種位置關系的相互轉化以及數量關系的求解.

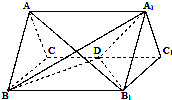 如圖,正三棱柱ABC-A1B1C1的所有棱長都為2,D為CC1的中點.
如圖,正三棱柱ABC-A1B1C1的所有棱長都為2,D為CC1的中點.


 備戰中考寒假系列答案
備戰中考寒假系列答案 如圖,正三棱柱ABC-A1B1C1各棱長都等于a,E是BB1的中點.
如圖,正三棱柱ABC-A1B1C1各棱長都等于a,E是BB1的中點. (2013•鄭州二模)如圖,正三棱柱ABC-A1B1C1的所有棱長都為2,D為CC1中點.
(2013•鄭州二模)如圖,正三棱柱ABC-A1B1C1的所有棱長都為2,D為CC1中點. 如圖,正三棱柱ABC-A1B1C1中(注:底面為正三角形且側棱與底面垂直),BC=CC1=2,P,Q分別為BB1,CC1的中點.
如圖,正三棱柱ABC-A1B1C1中(注:底面為正三角形且側棱與底面垂直),BC=CC1=2,P,Q分別為BB1,CC1的中點.