某單位有大會議室一間,室內面積共180平方米,擬分隔成兩類房間作為旅游客房:大房間每間面積為18 平方米,可住游客5名,每名游客每天住宿費為40元;小房間每間面積為15 平方米,可住游客3名,每名游客每天住宿費為50元.裝修大房間每間需1000元,裝修小房間每間需500元,如果裝修費用控制在8000元以內,假設游客能住滿客房,為獲得最大收益,那么應隔出大房間和小房間各多少間?每天最大收益是多少元?
解:設隔出大、小房間分別為x間,y間,
收益為z元,則z=200x+150y,-----(2分)
其中x、y為整數且滿足
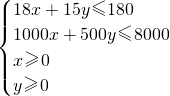
即
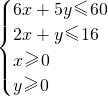
-----(10分)
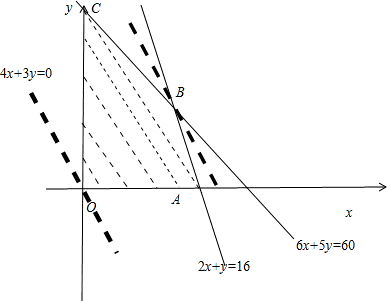
作出不等式組表示的平面區域,如圖所示的陰影部分為可行域.
由圖解法易知z=200x+150y過B時,目標函數z取得最大值
由
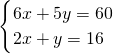
可得B(5,6),此時z=1900元,
即 5間18 平方米,6間15 平方米,此時收益最大,最大收益是1900元.-----(14分)
分析:先設隔出大、小房間分別為x間、y間,收益為Z元,寫出約束條件、目標函數,欲求收益最大值的,用直線平移法求出最優解,最后要將所求最優解還原為實際問題.
點評:本題主要考查了簡單線性規劃的應用.在解決線性規劃的應用題時,關鍵需要分析題目中相關量的關系,列出不等式組,即約束條件,由約束條件畫出可行域,分析目標函數Z與直線截距之間的關系,使用平移直線法求出最優解,還原到現實問題中.

 解:設隔出大、小房間分別為x間,y間,
解:設隔出大、小房間分別為x間,y間,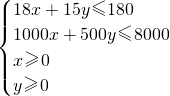
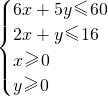 -----(10分)
-----(10分)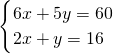 可得B(5,6),此時z=1900元,
可得B(5,6),此時z=1900元,
