
【題目】如圖,在平面直角坐標系中,已知橢圓C:![]() (a>b>0)的短軸長為2,F1,F2分別是橢圓C的左、右焦點,過點F2的動直線與橢圓交于點P,Q,過點F2與PQ垂直的直線與橢圓C交于A、B兩點.當直線AB過原點時,PF1=3PF2.
(a>b>0)的短軸長為2,F1,F2分別是橢圓C的左、右焦點,過點F2的動直線與橢圓交于點P,Q,過點F2與PQ垂直的直線與橢圓C交于A、B兩點.當直線AB過原點時,PF1=3PF2.
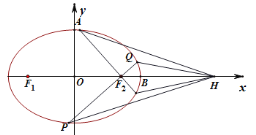
(1)求橢圓的標準方程;
(2)若點H(3,0),記直線PH,QH,AH,BH的斜率依次為![]() ,
,![]() ,
,![]() ,
,![]() .
.
①若![]() ,求直線PQ的斜率;
,求直線PQ的斜率;
②求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)①
(2)①![]() 或
或![]() ②
②![]()
【解析】
(1)已知條件有![]() ,直線AB過原點時,PQx軸,所以△PF1F2為直角三角形,利用橢圓定義和勾股定理可求得
,直線AB過原點時,PQx軸,所以△PF1F2為直角三角形,利用橢圓定義和勾股定理可求得![]() ,得橢圓方程;
,得橢圓方程;
(2)①設直線PQ:![]() ,代入到橢圓方程得后化簡,設P(
,代入到橢圓方程得后化簡,設P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),應用韋達定理得
),應用韋達定理得![]() ,
,![]() ,計算
,計算![]() 并代入
并代入![]() 可得;
可得;
②分類討論,當這兩條直線中有一條與坐標軸垂直時,![]() ,
,
當兩條直線與坐標軸都不垂直時,由①知![]() ,同理可得
,同理可得![]() ,計算
,計算![]() 后應用基本不等式可得最小值.
后應用基本不等式可得最小值.
解:(1)因為橢圓C:![]() (a>b>0)的短軸長為2,所以b=1,
(a>b>0)的短軸長為2,所以b=1,
當直線AB過原點時,PQx軸,所以△PF1F2為直角三角形,
由定義知PF1+PF2=2a,而PF1=3PF2,故![]() ,
,![]() ,
,
由![]() 得
得![]() ,化簡得a2=2,
,化簡得a2=2,
故橢圓的方程為![]() .
.
(2)①設直線PQ:![]() ,代入到橢圓方程得:
,代入到橢圓方程得:![]() ,設P(
,設P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),則
),則![]() ,
,![]() ,
,
所以![]()
![]()
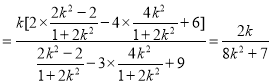
所以![]() ,
,
解得:![]() 或
或![]() ,即為直線PQ的斜率.
,即為直線PQ的斜率.
②當這兩條直線中有一條與坐標軸垂直時,![]() ,
,
當兩條直線與坐標軸都不垂直時,
由①知![]() ,同理可得
,同理可得![]()
故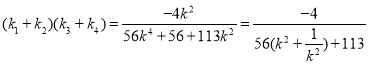
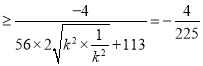 ,
,
當且僅當![]() 即k=1時取等號.
即k=1時取等號.
綜上,![]() 的最小值為
的最小值為![]() .
.


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() (
(![]() )的左、右焦點分別為
)的左、右焦點分別為![]() 、
、![]() ,離心率為
,離心率為![]() ,點P是橢圓C上的一個動點,且
,點P是橢圓C上的一個動點,且![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓C的方程;
(2)橢圓C與x軸交于A、B兩點,直線![]() 和
和![]() 與直線l:
與直線l:![]() 分別交于點M,N,試探究以
分別交于點M,N,試探究以![]() 為直徑的圓是否恒過定點,若是,求出所有定點的坐標:若否,請說明理由.
為直徑的圓是否恒過定點,若是,求出所有定點的坐標:若否,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
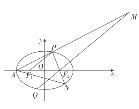
【題目】已知橢圓![]() 的左頂點為
的左頂點為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,離心率為
,離心率為![]() ,
,![]() 是橢圓上的一個動點(不與左、右頂點重合),且
是橢圓上的一個動點(不與左、右頂點重合),且![]() 的周長為6,點
的周長為6,點![]() 關于原點的對稱點為
關于原點的對稱點為![]() ,直線
,直線![]() 交于點
交于點![]() .
.
(1)求橢圓方程;
(2)若直線![]() 與橢圓交于另一點
與橢圓交于另一點![]() ,且
,且![]() ,求點
,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
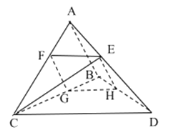
【題目】已知三棱錐![]() 中,
中,![]() 與
與![]() 均為等腰直角三角形,且
均為等腰直角三角形,且![]() ,
,![]() ,
,![]() 為
為![]() 上一點,且
上一點,且![]() 平面
平面![]() .
.
(1)求證:![]() ;
;
(2)過![]() 作一平面分別交
作一平面分別交![]() ,
, ![]() ,
, ![]() 于
于![]() ,
,![]() ,
,![]() ,若四邊形
,若四邊形![]() 為平行四邊形,求多面體
為平行四邊形,求多面體![]() 的表面積.
的表面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國在歐洲的某孔子學院為了讓更多的人了解中國傳統文化,在當地舉辦了一場由當地人參加的中國傳統文化知識大賽,為了了解參加本次大賽參賽人員的成績情況,從參賽的人員中隨機抽取![]() 名人員的成績(滿分100分)作為樣本,將所得數據進行分析整理后畫出頻率分布直方圖如圖所示,已知抽取的人員中成績在[50,60)內的頻數為3.
名人員的成績(滿分100分)作為樣本,將所得數據進行分析整理后畫出頻率分布直方圖如圖所示,已知抽取的人員中成績在[50,60)內的頻數為3.
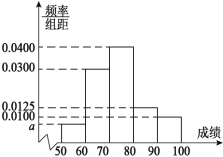
(1)求![]() 的值和估計參賽人員的平均成績(保留小數點后兩位有效數字);
的值和估計參賽人員的平均成績(保留小數點后兩位有效數字);
(2)已知抽取的![]() 名參賽人員中,成績在[80,90)和[90,100]女士人數都為2人,現從成績在[80,90)和[90,100]的抽取的人員中各隨機抽取2人,記這4人中女士的人數為
名參賽人員中,成績在[80,90)和[90,100]女士人數都為2人,現從成績在[80,90)和[90,100]的抽取的人員中各隨機抽取2人,記這4人中女士的人數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() :
:![]() 的離心率
的離心率![]() ,其左焦點
,其左焦點![]() 到此雙曲線漸近線的距離為
到此雙曲線漸近線的距離為![]() .
.
(1)求雙曲線![]() 的方程;
的方程;
(2)若過點![]() 的直線
的直線![]() 交雙曲線
交雙曲線![]() 于
于![]() 兩點,且以
兩點,且以![]() 為直徑的圓
為直徑的圓![]() 過原點
過原點![]() ,求圓
,求圓![]() 的圓心到拋物線
的圓心到拋物線![]() 的準線的距離.
的準線的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣a|﹣|x﹣5|.
(1)當a=2時,求證:﹣3≤f(x)≤3;
(2)若關于x的不等式f(x)≤x2﹣8x+20在R恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com