
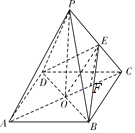
【題目】如圖所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面邊長為a,E是PC的中點.
(Ⅰ)求證:PA∥平面BDE;
(Ⅱ)平面PAC⊥平面BDE;
(Ⅲ)若二面角E-BD-C為30°,求四棱錐P-ABCD的體積.
【答案】(I)詳見解析;(II)詳見解析;(III)![]() .
.
【解析】
(Ⅰ)連接![]() ,證明
,證明![]() .然后證明
.然后證明![]() 平面
平面![]()
(Ⅱ)證明![]() ,
,![]() ,推出
,推出![]() 平面
平面![]() ,然后證明平面
,然后證明平面![]() ⊥平面
⊥平面![]()
(Ⅲ)取![]() 中點
中點![]() ,連接
,連接![]() ,說明
,說明![]() 為二面角
為二面角![]() 的平面角,求出
的平面角,求出![]() ,
,![]() ,
,![]() .然后求解幾何體的體積
.然后求解幾何體的體積
解:(Ⅰ)證明:連接OE,如圖所示.
∵O、E分別為AC、PC中點,
∴OE∥PA.
∵OE![]() 面BDE,PA
面BDE,PA![]() 平面BDE,
平面BDE,
∴PA∥平面BDE.
(Ⅱ)證明:∵PO⊥平面ABCD,∴PO⊥BD.
在正方形ABCD中,BD⊥AC,
又∵PO∩AC=O,∴BD⊥平面PAC.
又∵BD平面BDE,∴平面PAC⊥平面BDE.
(Ⅲ)取OC中點F,連接EF.
∵E為PC中點,
∴EF為△POC的中位線,∴EF∥PO.
又∵PO⊥平面ABCD,
∴EF⊥平面ABCD,
∵OF⊥BD,∴OE⊥BD.
∴∠EOF為二面角E-BD-C的平面角,
∴∠EOF=30°.
在Rt△OEF中,
OF=![]() OC=
OC=![]() AC=
AC=![]() a,
a,
∴EF=OFtan30°=![]() a,∴OP=2EF=
a,∴OP=2EF=![]() a.
a.
∴VP-ABCD=![]() ×a2×
×a2×![]() a=
a=![]() a3.
a3.


 狀元及第系列答案
狀元及第系列答案 同步奧數系列答案
同步奧數系列答案科目:高中數學 來源: 題型:
【題目】已知![]() f.
f.
(1)如果函數![]() 的單調遞減區間為
的單調遞減區間為![]() ,求函數
,求函數![]() 的解析式;
的解析式;
(2)在(1)的條件下,求函數![]() 的圖象在點
的圖象在點![]() 處的切線方程;
處的切線方程;
(3)若不等式![]() 恒成立,求實數a的取值范圍.
恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC⊥CB,點M和N分別是B1C1和BC的中點.

(1)求證:MB∥平面AC1N;
(2)求證:AC⊥MB.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】AC為對稱軸的拋物線的一部分,點B到邊AC的距離為2km,另外兩邊AC,BC的長度分別為8km,2 ![]() km.現欲在此地塊內建一形狀為直角梯形DECF的科技園區.
km.現欲在此地塊內建一形狀為直角梯形DECF的科技園區. 
(1)求此曲邊三角形地塊的面積;
(2)求科技園區面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】綠色出行越來越受到社會的關注,越來越多的消費者對新能源汽車感興趣![]() 但是消費者比較關心的問題是汽車的續駛里程
但是消費者比較關心的問題是汽車的續駛里程![]() 某研究小組從汽車市場上隨機抽取20輛純電動汽車調查其續駛里程
某研究小組從汽車市場上隨機抽取20輛純電動汽車調查其續駛里程![]() 單次充電后能行駛的最大里程
單次充電后能行駛的最大里程![]() ,被調查汽車的續駛里程全部介于50公里和300公里之間,將統計結果分成5組:
,被調查汽車的續駛里程全部介于50公里和300公里之間,將統計結果分成5組: ![]() ,繪制成如圖所示的頻率分布直方圖.
,繪制成如圖所示的頻率分布直方圖.
![]() 求直方圖中m的值;
求直方圖中m的值;
![]() 求本次調查中續駛里程在
求本次調查中續駛里程在![]() 的車輛數;
的車輛數;
![]() 若從續駛里程在
若從續駛里程在![]() 的車輛中隨機抽取2輛車,求其中恰有一輛車續駛里程在
的車輛中隨機抽取2輛車,求其中恰有一輛車續駛里程在![]() 的概率.
的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|2x﹣ ![]() |,其在區間[0,1]上單調遞增,則a的取值范圍為( )
|,其在區間[0,1]上單調遞增,則a的取值范圍為( )
A.[0,1]
B.[﹣1,0]
C.[﹣1,1]
D.[﹣ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某上市股票在30天內每股的交易價格![]() (元)與時間
(元)與時間![]() (天)組成有序數對
(天)組成有序數對![]() ,點
,點![]() 落在圖中的兩條線段上;該股票在30天內的日交易量
落在圖中的兩條線段上;該股票在30天內的日交易量![]() (萬股)與時間
(萬股)與時間![]() (天)的部分數據如下表所示,且
(天)的部分數據如下表所示,且![]() 與
與![]() 滿足一次函數關系,
滿足一次函數關系,

第 | 4 | 10 | 16 | 22 |
| 36 | 30 | 24 | 18 |
那么在這30天中第幾天日交易額最大( )
A. 10 B. 15 C. 20 D. 25
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】邗江中學高二年級某班某小組共10人,利用寒假參加義工活動,已知參加義工活動次數為1,2,3的人數分別為3,3,4.現從這10人中選出2人作為該組代表參加座談會.
(1)記“選出2人參加義工活動的次數之和為4”為事件![]() ,求事件
,求事件![]() 發生的概率;
發生的概率;
(2)設![]() 為選出2人參加義工活動次數之差的絕對值,求隨機變量
為選出2人參加義工活動次數之差的絕對值,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com