
【題目】已知函數![]() 的最小正周期為
的最小正周期為![]() ,且當
,且當![]() 時,
時, ![]() 取得最大值
取得最大值![]() .
.
(1)求![]() 的解析式及單調增區間;
的解析式及單調增區間;
(2)若![]() ,且
,且![]() ,求
,求![]() ;
;
(3)將函數![]() 的圖象向右平移
的圖象向右平移![]() (
(![]() )個單位長度后得到函數
)個單位長度后得到函數![]() 是偶函數,求
是偶函數,求![]() 的最小值.
的最小值.
【答案】(1)![]() (
(![]() );(2)
);(2)![]() ,
, ![]() ,
, ![]() 或
或![]() ;(3)
;(3)![]()
【解析】試題分析:(1)利用函數的周期、最值,求出![]() ,然后求出
,然后求出![]() ,通過當
,通過當![]() 時,
時, ![]() 取得最大值
取得最大值![]() ,求出
,求出![]() ,從而求
,從而求![]() 的解析式,解不等式
的解析式,解不等式![]() 可得單調增區間;(2)若
可得單調增區間;(2)若![]() ,且
,且![]() ,可得
,可得![]() 或
或![]() ,
, ![]() 取特殊值可求出
取特殊值可求出![]() ;(3)利用函數
;(3)利用函數![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后得到函數
個單位長度后得到函數![]() 的圖象,由
的圖象,由![]() 是偶函數,可得
是偶函數,可得![]() (
(![]() ),解得
),解得![]() ,然后再求
,然后再求![]() 的最小值.
的最小值.
試題解析:(1)由已知條件知, ![]() ,
, ![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() .
.
由![]() (
(![]() ) ,得
) ,得![]() (
(![]() )
)
所以![]() 的單調增區間是
的單調增區間是![]() (
(![]() )
)
(2)由![]() ,得
,得![]() ,
,
所以![]() 或
或![]() (
(![]() )
)
所以![]() 或
或![]() (
(![]() )
)
又![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() 或
或![]() .
.
(3)有條件,可得![]()
又![]() 是偶函數,所以
是偶函數,所以![]() 的圖象關于
的圖象關于![]() 軸對稱,所以當
軸對稱,所以當![]() 時,
時, ![]() 取最大值或最小值.
取最大值或最小值.
即![]() ,所以
,所以![]() (
(![]() ),解得
),解得![]() (
(![]() )
)
又![]() ,所以
,所以![]() 的最小值是
的最小值是![]() .
.


科目:高中數學 來源: 題型:
【題目】在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E、F分別為A1C1、B1C1的中點,D為棱CC1上任一點.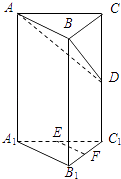
(Ⅰ)求證:直線EF∥平面ABD;
(Ⅱ)求證:平面ABD⊥平面BCC1B1 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+(x﹣1)ex .
(1)當a=﹣ ![]() 時,求f(x)在點P(1,f(1))處的切線方程;
時,求f(x)在點P(1,f(1))處的切線方程;
(2)討論f(x)的單調性;
(3)當﹣ ![]() <a<﹣
<a<﹣ ![]() 時,f(x)是否存在極值?若存在,求所有極值的和的取值范圍.
時,f(x)是否存在極值?若存在,求所有極值的和的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】濮陽市黃河灘區某村2010年至2016年人均純收入(單位:萬元)的數據如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代號x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y關于x的線性回歸方程;
(Ⅱ)利用(Ⅰ)中的回歸方程,分析2010年至2016年該村人均純收入的變化情況,并預測該村2017年人均純收入.
附:回歸直線的斜率和截距的最小乘法估計公式分別為: ![]() =
=  ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三個內角A,B,C所對應的邊分別為a,b,c,且滿足bcosC+ ![]() c=a.
c=a.
(1)求△ABC的內角B的大小;
(2)若△ABC的面積S= ![]() b2 , 試判斷△ABC的形狀.
b2 , 試判斷△ABC的形狀.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com