【題目】已知角α終邊逆時針旋轉 
與單位圓交于點 
，且 
．
（1）求 
的值，
（2）求 
的值．
【答案】
（1）解：角α終邊逆時針旋轉 
與單位圓交于點 
，
可得sin（ 
）= 
，
cos（ ）= 
，
sin（2 
）=2sin（ ）cos（ ）= 
= 
，
cos（2 ）=2× 
= 
．
=sin（2 ﹣ ）=sin（2 ）cos ﹣sin cos（2 ）= 
= 
．
（2）解：∵ 
，∴tan（2α+2β）= 
= 
= 
．
sin（2 ）= ，
cos（2 ）= ．
tan（2 ）= 
．
tan（2α+2β）=tan[（ 
）+（2 
）]= 
= ，
解得 
= 
【解析】（1）利用已知條件求出sin（ ）與cos（ ），然后利用二倍角公式以及兩角和的正弦函數化簡求解即可．（2）求出正切函數的二倍角的值，利用兩角和的正切函數化簡求解即可．
勵耘書業暑假銜接寧波出版社系列答案科目：高中數學 來源： 題型：
【題目】解答
（1）在公比為2的等比數列{an}中，a2與a5的等差中項是9 
．求a1的值；
（2）若函數y=a1sin（ 
φ），0＜φ＜π的一部分圖象如圖所示，M（﹣1，a1），N（3，﹣a1）為圖象上的兩點，設∠MON=θ，其中O為坐標原點，0＜θ＜π，求cos（θ﹣φ）的值．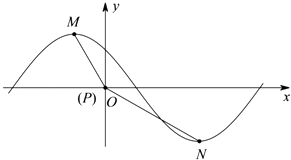 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在斜三棱柱ABC﹣A1B1C1中，側面ACC1A1與側面CBB1C1都是菱形，∠ACC1=∠CC1B1=60°，AC=2．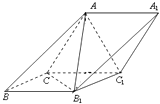 
（1）求證：AB1⊥CC1；
（2）若 
，求二面角C﹣AB1﹣A1的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】直線AB為圓的切線，切點為B，點C在圓上，∠ABC的角平分線BE交圓于點E，DB垂直BE交圓于點D．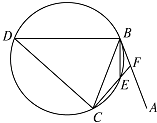 
（1）證明：DB=DC；
（2）設圓的半徑為1，BC=3，延長CE交AB于點F，求△BCF外接圓的半徑．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某房地產開發公司計劃在一樓區內建造一個長方形公園ABCD，公園由形狀為長方形A1B1C1D1的休閑區和環公園人行道(陰影部分)組成．已知休閑區A1B1C1D1的面積為4000平方米，人行道的寬分別為4米和10米(如圖所示)．
(1)若設休閑區的長和寬的比
＝x(x>1)，求公園ABCD所占面積S關于x的函數S(x)的解析式；
(2)要使公園所占面積最小，則休閑區A1B1C1D1的長和寬該如何設計？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖放置的邊長為2的正三角形
沿
軸滾動, 設頂點
的縱坐標與橫坐標的函數關系式是
， 有下列結論:
①函數的值域是
；②對任意的
，都有
；
③函數是偶函數；④函數單調遞增區間為
.
其中正確結論的序號是________. (寫出所有正確結論的序號)
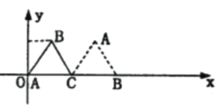
說明:
“正三角形沿軸滾動”包括沿軸正方向和沿軸負方向滾動. 沿軸正方向滾動指的是先以頂點
為中心順時針旋轉, 當頂點
落在軸上時, 再以頂點為中心順時針旋轉, 如此繼續. 類似地, 正三角形可以沿軸負方向滾動.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
