
【題目】已知直線l1:x﹣y+3=0和l2:x+y+1=0的交點為A,過A且與x軸和y軸都相切的圓的方程為_____,動點B,C分別在l1和l2上,且|BC|=2,則過A,B,C三點的動圓掃過的區域的面積為_____.
【答案】(x+1)2+(y﹣1)2=1或(x+5)2+(y+5)2=25; 4π.
【解析】
對于第一空:由兩直線的方程求出交點![]() 的坐標,設要求圓的方程為
的坐標,設要求圓的方程為![]() ,把點
,把點![]() 的坐標代入,可得
的坐標代入,可得![]() ,解可得
,解可得![]() 的值,即可得圓的方程;
的值,即可得圓的方程;
對于第二空:由直線的方程分析可得直線![]() 和
和![]() 垂直,進而分析可得過
垂直,進而分析可得過![]() 三點的動圓的圓心為
三點的動圓的圓心為![]() 的中點,其半徑
的中點,其半徑![]() ,進而可得動圓圓心的軌跡,據此分析可得答案.
,進而可得動圓圓心的軌跡,據此分析可得答案.
由題意,![]() ,解得:
,解得:![]()
可得直線![]() 和
和![]() 的交點為
的交點為![]() ,
,
顯然,點![]() 位于第二象限.
位于第二象限.
過![]() 且與
且與![]() 軸和
軸和![]() 軸都相切的圓的方程為
軸都相切的圓的方程為![]() ,
,
把點![]() 的坐標代入,可得
的坐標代入,可得![]() ,求得
,求得![]() ,或
,或 ![]() ,
,
故要求的圓的方程為![]() ,或者
,或者 ![]() ;
;
直線![]() 和
和![]() ,有1×1+
,有1×1+![]() ×1=0,則有直線
×1=0,則有直線![]() .
.
又由兩直線的交點為![]() ,動點
,動點![]() 分別在
分別在![]() 和
和![]() 上,且
上,且![]()
則過![]() 三點的動圓的圓心為
三點的動圓的圓心為![]() 的中點,其半徑
的中點,其半徑![]()
即動圓的圓心到![]() 的距離
的距離![]() ,
,
則動圓的圓心在以![]() 為圓心,半徑
為圓心,半徑![]() 的圓上,
的圓上,
故動圓掃過的區域的面積![]() ;
;
故答案為: ![]() 或者
或者![]() ;
; ![]() .
.


科目:高中數學 來源: 題型:
【題目】等差數列{an}的前n項和為Sn,a2+a15=17,S10=55.數列{bn}滿足an=log2bn.
(1)求數列{bn}的通項公式;
(2)若數列{an+bn}的前n項和Tn滿足Tn=S32+18,求n的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,在新高考改革中,打破文理分科的“![]() ”模式初露端倪,其中語、數、外三門課為必考科目,剩下三門為選考科目選考科目成績采用“賦分制”,即原始分數不直接用,而是按照學生分數在本科目考試的排名來劃分等級并以此打分得到最后得分,假定
”模式初露端倪,其中語、數、外三門課為必考科目,剩下三門為選考科目選考科目成績采用“賦分制”,即原始分數不直接用,而是按照學生分數在本科目考試的排名來劃分等級并以此打分得到最后得分,假定![]() 省規定:選考科目按考生成績從高到低排列,按照占總體
省規定:選考科目按考生成績從高到低排列,按照占總體![]() 、
、![]() 、
、![]() 、
、![]() 分別賦分
分別賦分![]() 分、
分、![]() 分、
分、![]() 分、
分、![]() 分,為了讓學生們體驗“賦分制”計算成績的方法,
分,為了讓學生們體驗“賦分制”計算成績的方法,![]() 省某高中高一(
省某高中高一(![]() )班(共
)班(共![]() 人)舉行了以此摸底考試(選考科目全考,單料全班排名),知這次摸底考試中的物理成績(滿分
人)舉行了以此摸底考試(選考科目全考,單料全班排名),知這次摸底考試中的物理成績(滿分![]() 分)頻率分布直方圖,化學成績(滿分
分)頻率分布直方圖,化學成績(滿分![]() 分)莖葉圖如圖所示,小明同學在這次考試中物理
分)莖葉圖如圖所示,小明同學在這次考試中物理![]() 分,化學
分,化學![]() 多分.
多分.
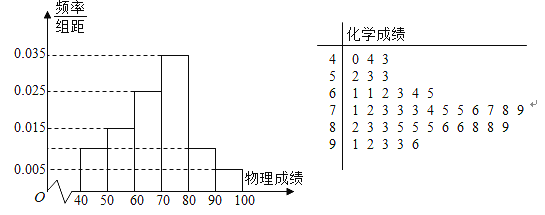
(1)采用賦分制后,求小明物理成績的最后得分;
(2)若小明的化學成績最后得分為![]() 分,求小明的原始成績的可能值;
分,求小明的原始成績的可能值;
(3)若小明必選物理,其他兩科從化學、生物、歷史、地理、政治五科中任選,求小明此次考試選考科目包括化學的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將正方形ABCD沿對角線BD折成直二面角A-BD-C,有如下四個結論
①AC⊥BD;
②△ACD是等邊三角形;
③AB與平面BCD成60°的角;
④AB與CD所成的角是60°.
其中正確結論的序號是________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其導函數為
,其導函數為![]() .
.
(1)當![]() ,求
,求![]() 圖象在
圖象在![]() 處的切線方程;
處的切線方程;
(2)設![]() 在定義域上是單調函數,求
在定義域上是單調函數,求![]() 得取值范圍;
得取值范圍;
(3)若![]() 的極大值和極小值分別為
的極大值和極小值分別為![]() 、
、![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點M在橢圓![]() 1(0<b
1(0<b![]() )上,且位于第一象限,F1,F2為橢圓的兩個焦點,過F1,F2,M的圓與y軸交于點P,Q(P在Q的上方),|OP||OQ|=1.
)上,且位于第一象限,F1,F2為橢圓的兩個焦點,過F1,F2,M的圓與y軸交于點P,Q(P在Q的上方),|OP||OQ|=1.
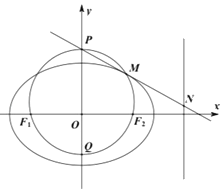
(Ⅰ)求b的值;
(Ⅱ)直線PM與直線x=2交于點N,試問,在x軸上是否存在定點T,使得![]()
![]() 為定值?若存在,求出點T的坐標與該定值;若不存在,請說明理由.
為定值?若存在,求出點T的坐標與該定值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,右焦點為
,右焦點為![]() ,直線l經過點F,且與橢圓交于A,B兩點,O為坐標原點.
,直線l經過點F,且與橢圓交于A,B兩點,O為坐標原點.
(1)求橢圓的標準方程;
(2)當直線l繞點F轉動時,試問:在x軸上是否存在定點M,使得![]() 為常數?若存在,求出定點M的坐標;若不存在,請說明理由.
為常數?若存在,求出定點M的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com