
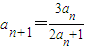 (n∈N*).
(n∈N*).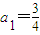 ,計算a2,a3,a4的值,并求出數列的通項公式;
,計算a2,a3,a4的值,并求出數列的通項公式;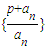 成等比數列.
成等比數列. 化簡后,可求出an的值與an>0,an≠1矛盾,所以假設錯誤,原結論正確;
化簡后,可求出an的值與an>0,an≠1矛盾,所以假設錯誤,原結論正確;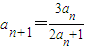 中,由a1的值即可求出a2的值,把n=2代入
中,由a1的值即可求出a2的值,把n=2代入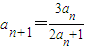 中,由a2的值即可求出a3的值,把n=4代入
中,由a2的值即可求出a3的值,把n=4代入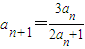 中,由a3的值即可求出a4的值,把已知的等式去分母后,在變形后的式子等號兩邊都除以3anan+1,變形后得到數列
中,由a3的值即可求出a4的值,把已知的等式去分母后,在變形后的式子等號兩邊都除以3anan+1,變形后得到數列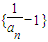 是等比數列,找出首項和公比寫出此等比數列的通項公式,化簡后即可得到數列的通項公式an;
是等比數列,找出首項和公比寫出此等比數列的通項公式,化簡后即可得到數列的通項公式an;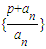 成等比數列,公比為q,根據等比數列的定義可知第n+1項與第n項的比值等于公比q,化簡后根據p不為0,利用多項式為0時,各項的系數都為0即可求出p與q的值.
成等比數列,公比為q,根據等比數列的定義可知第n+1項與第n項的比值等于公比q,化簡后根據p不為0,利用多項式為0時,各項的系數都為0即可求出p與q的值.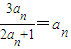 ,
, ,令n=1得:a2=
,令n=1得:a2=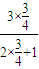 =
= ,
,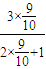 =
=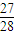 ,令n=3得:a4=
,令n=3得:a4=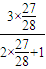 =
=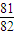 ,
,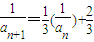 ,得
,得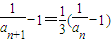 ,
,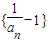 是首項為
是首項為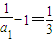 ,公比為
,公比為 的等比數列,
的等比數列,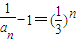 ,得
,得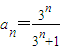 ;
; 成等比數列,公比為q,
成等比數列,公比為q,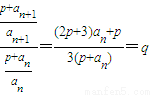 ,
,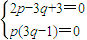 ,
,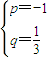 ,
,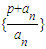 是公比為
是公比為 的等比數列.
的等比數列.

科目:高中數學 來源: 題型:
| 3an |
| 2an+1 |
| 3 |
| 4 |
| p+an |
| an |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
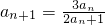 (n∈N*).
(n∈N*).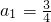 ,計算a2,a3,a4的值,并求出數列的通項公式;
,計算a2,a3,a4的值,并求出數列的通項公式;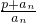 成等比數列.
成等比數列.查看答案和解析>>
科目:高中數學 來源:2011年上海市虹口區高考數學二模試卷(理科)(解析版) 題型:解答題
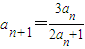 (n∈N*).
(n∈N*).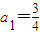 ,計算a2,a3,a4的值,并求出數列的通項公式;
,計算a2,a3,a4的值,并求出數列的通項公式;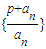 成等比數列.
成等比數列.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com