
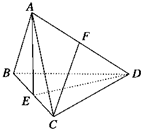
 解:如圖所示,平面ABC⊥平面BCD,△ABC與△BCD均為邊長為a的正三角形,
解:如圖所示,平面ABC⊥平面BCD,△ABC與△BCD均為邊長為a的正三角形, a2,AE=
a2,AE= a,
a, •
• a2•
a2• a=
a= a3.
a3. a,
a, •
• a=
a= a.
a. •
• a=
a= a,
a, a.
a. AD•CF=
AD•CF=
 a×
a× a=
a=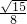 a2.
a2.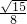 a2.
a2. a2+
a2+ a2+2×
a2+2×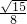 a2=
a2=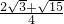 a2.
a2. S△BCD×AE即可求解.
S△BCD×AE即可求解.

 品學雙優卷系列答案
品學雙優卷系列答案 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com