
已知集合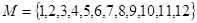 ,以下命題正確的序號是 .
,以下命題正確的序號是 .
①如果函數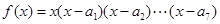 ,其中
,其中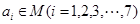 ,那么
,那么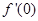 的最大值為
的最大值為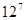 .
.
②數列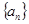 滿足首項
滿足首項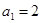 ,
,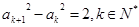 ,當
,當 且
且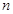 最大時,數列
最大時,數列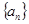 有2048個.
有2048個.
③數列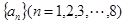 滿足
滿足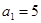 ,
, ,
,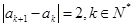 ,如果數列
,如果數列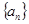 中的每一項都是集合M的元素,則符合這些條件的不同數列
中的每一項都是集合M的元素,則符合這些條件的不同數列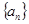 一共有33個.
一共有33個.
④已知直線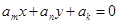 ,其中
,其中 ,而且
,而且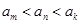 ,則一共可以得到不同的直線196條.
,則一共可以得到不同的直線196條.
②③④
解析試題分析:對①,將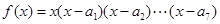 求導得:
求導得: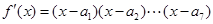
 ,所以
,所以 .故錯.
.故錯.
對②, 是一個等差數列,
是一個等差數列,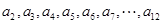 都是互為相反數的兩個值,所以數列
都是互為相反數的兩個值,所以數列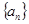 共有
共有 個.
個.
對③,由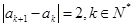 得
得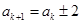 .
.
法一、由于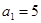 ,
, ,故將
,故將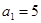 加4個2,再減3個2即可.由于
加4個2,再減3個2即可.由于 故不能連續加4次,也不能連續減3次,所以共有
故不能連續加4次,也不能連續減3次,所以共有 個.
個.
法二、因為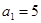 ,所以
,所以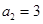 或
或 ,注意到數列
,注意到數列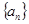 中的每一項都是集合M的元素,依次下去可得
中的每一項都是集合M的元素,依次下去可得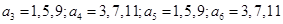 .由于
.由于 ,所以
,所以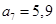 .由此我們可得以下樹圖:
.由此我們可得以下樹圖: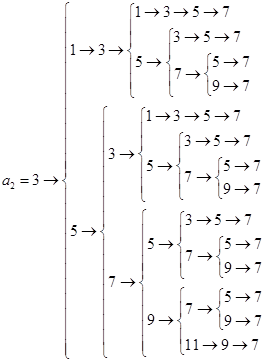 ,
,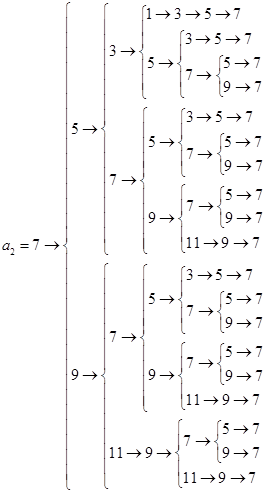
所以符合這些條件的不同數列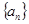 一共有14+19=33個.
一共有14+19=33個.
法三、由于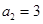 或
或 ,
,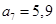 ,故可以分以下四種情況分別求解:
,故可以分以下四種情況分別求解: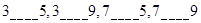 .
. ,共有9個;
,共有9個; ,共有5個;
,共有5個; ,共有10個;
,共有10個; ,共有9個.所以總共有33個.
,共有9個.所以總共有33個.
對④,從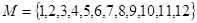 中取3個不同的數作為
中取3個不同的數作為 ,因為
,因為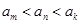 ,所以共有
,所以共有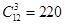 種取法.再排除其中重復的直線.與
種取法.再排除其中重復的直線.與 相同的有
相同的有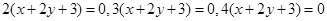 ,多3條;與
,多3條;與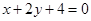 相同的有
相同的有 ,多2條;與
,多2條;與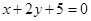 相同的有
相同的有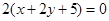 ,多1條;與
,多1條;與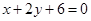 相同的有
相同的有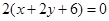 ,多1條;與
,多1條;與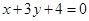 相同的有
相同的有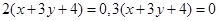 ,多2條;與
,多2條;與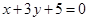 相同的有
相同的有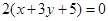 ,多1條;與
,多1條;與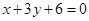 相同的有
相同的有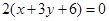 ,多1條;與
,多1條;與 相同的有
相同的有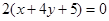 ,多1條;與
,多1條;與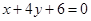 相同的有
相同的有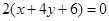 ,多1條;與
,多1條;與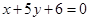 相同的有
相同的有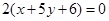 ,多1條;與
,多1條;與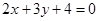 相同的有
相同的有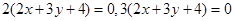 ,多2條;與
,多2條;與 相同的有
相同的有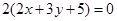 ,多1條;與
,多1條;與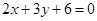 相同的有
相同的有 ,多1條;與
,多1條;與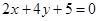 相同的有
相同的有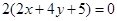 ,多1條;與
,多1條;與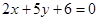 相同的有
相同的有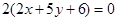 ,多1條(注意
,多1條(注意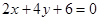 這種情況在前面已經考慮了);與
這種情況在前面已經考慮了);與 相同的有
相同的有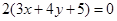 ,多1條;與
,多1條;與

科目:高中數學 來源: 題型:填空題
給出下列命題:
① 已知線性回歸方程 ,當變量
,當變量 增加2個單位,其預報值平均增加4個單位;
增加2個單位,其預報值平均增加4個單位;
② 在進制計算中, ;
;
③ 若 ,且
,且 ,則
,則 ;
;
④ “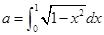 ”是“函數
”是“函數 的最小正周期為4”的充要條件;
的最小正周期為4”的充要條件;
⑤ 設函數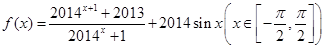 的最大值為M,最小值為m,則M+m=4027,其中正確命題的個數是 個。
的最大值為M,最小值為m,則M+m=4027,其中正確命題的個數是 個。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com