Question

（2013•茂名一模）已知x、y滿足約束條件

x+y≤3 x-y≥-1 y≥1

若0≤ax+by≤2，則

b+2

a+1

的取值范圍為（　　）

A．[0，1]

B．[1，10]

C．[1，3]

D．[2，3]

Answer 1

分析：作出題中不等式組對應的平面區域，得到如圖的△ABC及其內部，其中A（0，1），B（2，1），C（1，2）．因為不等式0≤ax+by≤2對約束條件的所有x、y都成立，所以可得關于a、b的不等式組成立，在aob坐標系內作出相應的平面區域并利用P（-1，-2）、Q（a，b）兩點連線的斜率，即可得到

b+2

a+1

的取值范圍．

解答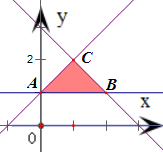：解：作出不等式組

x+y≤3 x-y≥-1 y≥1

表示的平面區域，
得到如圖的△ABC及其內部，其中A（0，1），B（2，1），C（1，2）
∵不等式0≤ax+by≤2對于約束條件的所有x、y都成立
∴記F（x，y）=ax+by，可得

F(0，1)=b∈[0，2] F(2，1)=2a+b∈[0，2] F(1，2)=a+2b∈[0，2]

即

0≤b≤2 0≤2a+b≤2 0≤a+2b≤2

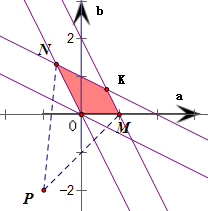
，在aob坐標系中作出不等式組表示的平面區域，
得到如圖的四邊形MKNO及其內部，
其中M（1，0），K（

2

3

，

2

3

），N（-

2

3

，

4

3

），O是坐標原點
而k=

b+2

a+1

表示點P（-1，-2）與Q（a，b）連線的斜率，
點Q是四邊形MKNO內部或邊界一點
運動點Q可得：當Q與M重合時，k達到最小值，k_min=

0+2

1+1

=1
當Q與N重合量，k達到最大值，k_max=

4 3 +2

- 2 3 +1

=10
∴

b+2

a+1

的取值范圍為[1，10]
故答案為：[1，10]

點評：本題給出二元一次不等式組，在0≤ax+by≤2恒成立的情況下，求

b+2

a+1

的取值范圍．著重考查了二元一次不等式組表示的平面區域、直線的斜率和簡單的線性規劃等知識，屬于基礎題．