
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為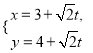 (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,并使得它與直角坐標系
軸的正半軸為極軸建立極坐標系,并使得它與直角坐標系![]() 有相同的長度單位,曲線
有相同的長度單位,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與直線
與直線![]() 交于
交于![]() 、
、![]() 兩點,且
兩點,且![]() 點的坐標為
點的坐標為![]() ,求
,求![]() 的值.
的值.
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的右焦點為
的右焦點為![]() ,過
,過![]() 且與
且與![]() 軸垂直的弦長為3.
軸垂直的弦長為3.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)過![]() 作直線
作直線![]() 與橢圓交于
與橢圓交于![]() 兩點,問:在
兩點,問:在![]() 軸上是否存在點
軸上是否存在點![]() ,使
,使![]() 為定值,若存在,請求出
為定值,若存在,請求出![]() 點坐標,若不存在,請說明理由.
點坐標,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
已知極坐標系的極點在直角坐標系的原點處,極軸與![]() 軸的非負半軸重合,直線
軸的非負半軸重合,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數),曲線
為參數),曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)設![]() ,
, ![]() 分別是直線
分別是直線![]() 與曲線
與曲線![]() 上的點,求
上的點,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以該橢圓上的點和橢圓的左、右焦點
,以該橢圓上的點和橢圓的左、右焦點![]() ,
,![]() 為頂點的三角形的周長為
為頂點的三角形的周長為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設該橢圓![]() 與
與![]() 軸的交點為
軸的交點為![]() ,
, ![]() (點
(點![]() 位于點
位于點![]() 的上方),直線
的上方),直線![]() 與橢圓
與橢圓![]() 相交于不同的兩點
相交于不同的兩點![]() ,求證:直線
,求證:直線![]() 與直線
與直線![]() 的交點
的交點![]() 在定直線上.
在定直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市縣鄉教師流失現象非常嚴重,為了縣鄉孩子們能接受良好教育,某市今年要為兩所縣鄉中學招聘儲備未來三年的教師,已知現在該市縣鄉中學無多余教師,為決策應招聘多少縣鄉教師搜集并整理了該市50所縣鄉中學在過去三年內的教師流失數,得到如表的頻率分布表:以這50所縣鄉中學流失教師數的頻率代替一所縣鄉中學流失教師數發生的概率.
(1)求該市所有縣鄉中學教師流失數不低于8的概率;
(2)若從上述50所縣鄉中學中流失教師數不低于9的縣鄉學校中任取兩所調查回訪,了解其中原因,求這兩所學校的教師流失數都是10的概率.
流失教師數 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
頻數 | 2 | 4 | 11 | 16 | 12 | 3 | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com