
【題目】在直角坐標(biāo)系![]() 中,圓
中,圓![]() 的方程為
的方程為![]() ,以坐標(biāo)原點
,以坐標(biāo)原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系,直線
軸的正半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求圓![]() 的極坐標(biāo)方程與直線
的極坐標(biāo)方程與直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)設(shè)直線![]() 與圓
與圓![]() 相交于
相交于![]() ,
,![]() 兩點,求圓
兩點,求圓![]() 在
在![]() ,
,![]() 處兩條切線的交點坐標(biāo).
處兩條切線的交點坐標(biāo).
【答案】(1)圓![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,直線
,直線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]() ;(2)
;(2)![]() .
.
【解析】
(1)由題意結(jié)合直角坐標(biāo)方程與極坐標(biāo)方程的轉(zhuǎn)化公式可得圓![]() 的極坐標(biāo)方程;轉(zhuǎn)化直線
的極坐標(biāo)方程;轉(zhuǎn)化直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,再利用直角坐標(biāo)方程與極坐標(biāo)方程的轉(zhuǎn)化公式即可得直線
,再利用直角坐標(biāo)方程與極坐標(biāo)方程的轉(zhuǎn)化公式即可得直線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(2)由題意聯(lián)立方程組可得![]() ,
,![]() 的坐標(biāo),結(jié)合直線與圓相切的性質(zhì)、直線方程的求解即可得兩切線方程,聯(lián)立方程即可得解.
的坐標(biāo),結(jié)合直線與圓相切的性質(zhì)、直線方程的求解即可得兩切線方程,聯(lián)立方程即可得解.
(1)圓![]() 的方程
的方程![]() 可變?yōu)?/span>
可變?yōu)?/span>![]() ,
,
所以圓![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() 即
即![]() ;
;
直線![]() 的極坐標(biāo)方程
的極坐標(biāo)方程![]() 可變?yōu)?/span>
可變?yōu)?/span>![]() ,
,
所以直線![]() 的直角坐標(biāo)方程為
的直角坐標(biāo)方程為![]() 即
即![]() ;
;
(2)由題意聯(lián)立方程組 ,解得
,解得![]() 或
或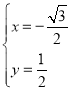 ,
,
不妨設(shè)點![]() ,
,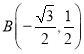 ,設(shè)過
,設(shè)過![]() ,
,![]() 處的切線分別為
處的切線分別為![]() ,
,![]() ,
,
圓![]() 的圓心為
的圓心為![]() ,半徑為
,半徑為![]() ,
,
易得![]() ,
,
由直線![]() 的斜率
的斜率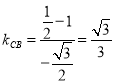 可得直線
可得直線![]() 的斜率
的斜率![]() ,
,
所以直線![]() 的方程為
的方程為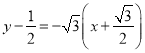 即
即![]() ,
,
由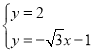 可得
可得 ,
,
所以圓![]() 在
在![]() ,
,![]() 處兩條切線的交點坐標(biāo)為
處兩條切線的交點坐標(biāo)為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 的前n項和為
的前n項和為![]() ,
,![]()
![]() ,若
,若![]() 是公差不為0的等差數(shù)列,且
是公差不為0的等差數(shù)列,且![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)證明:數(shù)列![]() 是等差數(shù)列;
是等差數(shù)列;
(3)記![]() ,若存在
,若存在![]() ,
,![]() (
(![]() ),使得
),使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】稠環(huán)芳香烴化合物中有不少是致癌物質(zhì),比如學(xué)生鐘愛的快餐油炸食品中會產(chǎn)生苯并芘,它是由一個苯環(huán)和一個芘分子結(jié)合而成的稠環(huán)芳香烴類化合物,長期食用會致癌.下面是一組稠環(huán)芳香烴的結(jié)構(gòu)簡式和分子式:
名稱 | 萘 | 蒽 | 并四苯 | … | 并n苯 |
結(jié)構(gòu)簡式 |
|
|
| … | … |
分子式 |
|
|
| … | … |
由此推斷并十苯的分子式為________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一款小游戲的規(guī)則如下:每輪游戲要進行三次,每次游戲都需要從裝有大小相同的2個紅球,3個白球的袋中隨機摸出2個球,若摸出的“兩個都是紅球”出現(xiàn)3次獲得200分,若摸出“兩個都是紅球”出現(xiàn)1次或2次獲得20分,若摸出“兩個都是紅球”出現(xiàn)0次則扣除10分(即獲得![]() 分).
分).
(1)設(shè)每輪游戲中出現(xiàn)“摸出兩個都是紅球”的次數(shù)為![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩過這款游戲的許多人發(fā)現(xiàn),若干輪游戲后,與最初的分?jǐn)?shù)相比,分?jǐn)?shù)沒有增加反而減少了,請運用概率統(tǒng)計的相關(guān)知識分析解釋上述現(xiàn)象.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】公元五世紀(jì),數(shù)學(xué)家祖沖之估計圓周率![]() 的值的范圍是:
的值的范圍是:![]() ,為紀(jì)念數(shù)學(xué)家祖沖之在圓周率研究上的成就,某教師在講授概率內(nèi)容時要求學(xué)生從小數(shù)點后的6位數(shù)字1,4,1,5,9,2中隨機選取兩個數(shù)字做為小數(shù)點后的前兩位(整數(shù)部分3不變),那么得到的數(shù)字大于3.14的概率為( )
,為紀(jì)念數(shù)學(xué)家祖沖之在圓周率研究上的成就,某教師在講授概率內(nèi)容時要求學(xué)生從小數(shù)點后的6位數(shù)字1,4,1,5,9,2中隨機選取兩個數(shù)字做為小數(shù)點后的前兩位(整數(shù)部分3不變),那么得到的數(shù)字大于3.14的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() ,
,![]() ,是橢圓
,是橢圓![]() 的左,右焦點,直線
的左,右焦點,直線![]() 與橢圓相交于
與橢圓相交于![]() ,
,![]() 兩點
兩點
(1)若線段![]() 的中點為
的中點為![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)若直線![]() 過橢圓
過橢圓![]() 的左焦點
的左焦點![]() ,
,![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以原點
為參數(shù)),以原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標(biāo)系,直線
軸的非負半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 與曲線
與曲線![]() 的普通方程;
的普通方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() 是偶函數(shù),且當(dāng)
是偶函數(shù),且當(dāng)![]() 時,
時,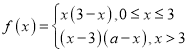
(1)當(dāng)![]() 時,求
時,求![]() 的解析式;
的解析式;
(2)設(shè)函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值為
上的最大值為![]() ,試求
,試求![]() 的表達式;
的表達式;
(3)若方程![]() 有四個不同的實根,且它們成等差數(shù)列,試探求
有四個不同的實根,且它們成等差數(shù)列,試探求![]() 與
與![]() 滿足的條件.
滿足的條件.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com