
【題目】已知函數f(x)=(ax2+bx+c)ex在[0,1]上單調遞減且滿足f(0)=1,f(1)=0.
(1)求a取值范圍;
(2)設g(x)=f(x)﹣f′(x),求g(x)在[0,1]上的最大值和最小值.
【答案】
(1)解:由f(0)=1,f(1)=0得c=1,a+b=﹣1,則f(x)=[ax2﹣(a+1)x+1]ex,
∴f′(x)=[ax2+(a﹣1)x﹣a]ex,
由題意函數f(x)=(ax2+bx+c)ex在[0,1]上單調遞減可得對于任意的x∈(0,1),都有f′(x)≤0
當a>0時,因為二次函數y=ax2+(a﹣1)x﹣a圖象開口向上,而f′(0)=﹣a<0,所以只需要f′(1)=(a﹣1)e≤0,即a≤1,故有0<a≤1;
當a=1時,對于任意的x∈(0,1),都有f′(x)=(x2﹣1)ex<0,函數符合條件;
當a=0時,對于任意的x∈(0,1),都有f′(x)=﹣xex<0,函數符合條件;
當a<0時,因f′(0)=﹣a>0函數不符合條件;
綜上知,a的取值范圍是0≤a≤1
(2)解:因為 g(x)=f(x)﹣f′(x)=(ax2﹣(a+1)x+1)ex﹣[ax2+(a﹣1)x﹣a]ex=(﹣2ax+a+1)ex,g′(x)=(﹣2ax﹣a+1)ex,
(i)當a=0時,g′(x)=ex>0,g(x)在[0,1]上的最小值是g(0)=1,最大值是g(1)=e
(ii)當a=1時,對于任意x∈(0,1)有g′(x)=﹣2xex<0,則有g(x)在[0,1]上的最小值是g(1)=0,最大值是g(0)=2;
(iii)當0<a<1時,由g′(x)=0得x= ![]() >0,
>0,
①若 ![]() ,即0<a≤
,即0<a≤ ![]() 時,g(x)在[0,1]上是增函數,所以g(x)在[0,1]上最大值是g(1)=(1﹣a)e,最小值是g(0)=1+a;
時,g(x)在[0,1]上是增函數,所以g(x)在[0,1]上最大值是g(1)=(1﹣a)e,最小值是g(0)=1+a;
②若 ![]() ,即
,即 ![]() <a<1時,g(x)在x=
<a<1時,g(x)在x= ![]() 取得最大值g(
取得最大值g( ![]() )=2a
)=2a ![]() ,在x=0或x=1時取到最小值,
,在x=0或x=1時取到最小值,
而g(0)=1+a,g(1)=(1﹣a)e,
則令g(0)=1+a≤g(1)=(1﹣a)e可得 ![]() <a≤
<a≤ ![]() ;令g(0)=1+a≥g(1)=(1﹣a)e可得
;令g(0)=1+a≥g(1)=(1﹣a)e可得 ![]() ≤a<1
≤a<1
綜上,當 ![]() <a≤
<a≤ ![]() 時,g(x)在x=0取到最小值g(0)=1+a,
時,g(x)在x=0取到最小值g(0)=1+a,
當 ![]() ≤a<1時,g(x)在x=1取到最小值g(1)=(1﹣a)e
≤a<1時,g(x)在x=1取到最小值g(1)=(1﹣a)e
【解析】(1)由題意,函數f(x)=(ax2+bx+c)ex在[0,1]上單調遞減且滿足f(0)=1,f(1)=0,可求出函數的導數,將函數在[0,1]上單調遞減轉化為導數在[0,1]上的函數值恒小于等于0,再結合f(0)=1,f(1)=0這兩個方程即可求得a取值范圍;(2)由題設條件,先給出g(x)=f(x)﹣f′(x)的解析式,求出導函數,g′(x)=(﹣2ax﹣a+1)ex , 由于參數a的影響,函數在[0,1]上的單調性不同,結合(1)的結論及g′(x)可得.(i)當a=0時;(ii)當a=1時;(iii)當0<a<1時,分三類對函數的單調性進行討論,確定并求出函數的最值
【考點精析】利用利用導數研究函數的單調性和函數的最大(小)值與導數對題目進行判斷即可得到答案,需要熟知一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:
【題目】某連鎖經營公司所屬5個零售店某月的銷售額和利潤額資料如表:
商店名稱 | A | B | C | D | E |
銷售額x/千萬元 | 3 | 5 | 6 | 7 | 9 |
利潤額y/百萬元 | 2 | 3 | 3 | 4 | 5 |
(1)畫出銷售額和利潤額的散點圖;
(2)若銷售額和利潤額具有相關關系,用最小二乘法計算利潤額y對銷售額x的回歸直線方程;
(3)據(2)的結果估計當銷售額為1億元時的利潤額.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對二次函數f(x)=ax2+bx+c(a為非零整數),四位同學分別給出下列結論,其中有且只有一個結論是錯誤的,則錯誤的結論是( )
A.﹣1是f(x)的零點
B.1是f(x)的極值點
C.3是f(x)的極值
D.點(2,8)在曲線y=f(x)上
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數y=Asin(ωx+φ)在一個周期內的圖象如圖,此函數的解析式為( ) 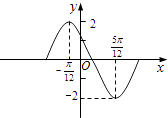
A.y=2sin(2x+ ![]() )??
)??
B.y=2sin(2x+ ![]() )??
)??
C.y=2sin( ![]() ﹣
﹣ ![]() )??
)??
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設m∈R,復數z=(m2﹣3m﹣4)+(m2+3m﹣28)i,其中i為虛數單位.
(1)當m為何值時,復數z是虛數?
(2)當m為何值時,復數z是純虛數?
(3)當m為何值時,復數z所對應的點在復平面內位于第四象限?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 上是減函數,求實數
上是減函數,求實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,分別求函數
時,分別求函數![]() 的最小值和
的最小值和![]() 的最大值,并證明當
的最大值,并證明當![]() 時,
時, ![]() 成立;
成立;
(3)令![]() ,當
,當![]() 時,判斷函數
時,判斷函數![]() 有幾個不同的零點并證明.
有幾個不同的零點并證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{bn}滿足bn=3bn﹣1+2(n≥2),b1=1.數列{an}的前n項和為Sn , 滿足Sn=4an+2
(1)求證:{bn+1}是等比數列并求出數列{bn}的通項公式;
(2)求數列{an}的通項公式和前n項和公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓O:x2+y2=r2(r>0),點P為圓O上任意一點(不在坐標軸上),過點P作傾斜角互補的兩條直線分別交圓O于另一點A,B.
(1)當直線PA的斜率為2時,
①若點A的坐標為(﹣ ![]() ,﹣
,﹣ ![]() ),求點P的坐標;
),求點P的坐標;
②若點P的橫坐標為2,且PA=2PB,求r的值;
(2)當點P在圓O上移動時,求證:直線OP與AB的斜率之積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC中,BC邊上的高所在的直線方程為x﹣2y+1=0,∠A的角平分線所在的直線方程為y=0,點C的坐標為(1,2).
(1)求點A和點B的坐標;
(2)又過點C作直線l與x軸、y軸的正半軸分別交于點M,N,求△MON的面積最小值及此時直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com