
在各項均為負數的數列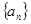 中,已知點
中,已知點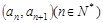 在函數
在函數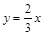 的圖像上,且
的圖像上,且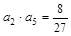 .
.
(Ⅰ)求證:數列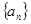 是等比數列,并求出其通項;
是等比數列,并求出其通項;
(Ⅱ)若數列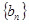 的前
的前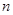 項和為
項和為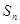 ,且
,且 ,求
,求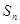 .
.
(1)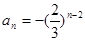 ;(2)
;(2)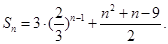 .
.
【解析】本題考查等比數列的概念、通項,等比數列和等差數列的求和。高考對數列的考查難度在下降,其考查的重點轉變為考查數列中的基本問題、兩類基本數列,以及數列求和方面。解決兩類基本數列問題的一個重要思想是基本量方法,即通過列出方程或者方程組求出等差數列的首項和公差、等比數列的首項和公比。數列求和要掌握好三個方法,一個是本題使用的分組求和,第二個是錯位相減法,第三個是裂項求和法。(1)把點的坐標代入直線方程,根據等比數列的定義進行證明,顯然公比是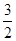 ,再根據條件
,再根據條件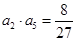 求出首項即可求出這個數列的通項公式;(2)數列
求出首項即可求出這個數列的通項公式;(2)數列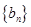 是一個等比數列和一個等差數列的對應項的和組成的數列,分別求和即可。
是一個等比數列和一個等差數列的對應項的和組成的數列,分別求和即可。
解:(1)因為點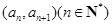 在函數
在函數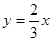 的圖像上,所以
的圖像上,所以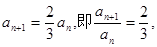 故數列
故數列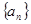 是公比
是公比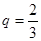 的等比數列因為
的等比數列因為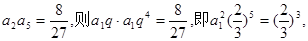 由于數列
由于數列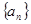 的各項均為負數,則
的各項均為負數,則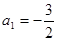 所以
所以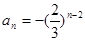 ………….6分
………….6分
(2)由(1)知,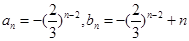 ,所以
,所以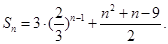 …12分
…12分


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:高中數學 來源: 題型:
| 2 |
| 3 |
| 8 |
| 27 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| 3 |
| 8 |
| 27 |
| 2 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 8 |
| 27 |
| 16 |
| 81 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
| 3 |
| 8 |
| 27 |
查看答案和解析>>
科目:高中數學 來源:2011屆山東省萊蕪一中高三上學期期末考試數學理卷 題型:解答題
(本小題滿分12分)
在各項均為負數的數列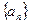 中,已知點
中,已知點 在
在 函數
函數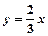 的圖像上,且
的圖像上,且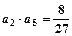 .
.
(1)求證:數列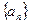 是等比數列,并求出其通項;
是等比數列,并求出其通項;
(2)若數列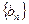 的前
的前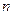 項和為
項和為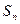 ,且
,且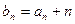 ,求
,求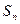 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com