
分析 (1)由S n+1=4an+2(n∈N•),可得n=1時,a1+a2=4a1+2,解得a2.n≥2時,an+1=Sn+1-Sn,化為:an+1=4an-4an-1,變形為:an+1-2an=2(an-2an-1),可得bn=2bn-1.即可證明.
(2)由(1)可得:bn=3×2n-1.an+1-2an=3×2n-1,可得$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=$\frac{3}{4}$.利用等差數列與等比數列的通項公式即可得出.
解答 證明:(1)∵S n+1=4an+2(n∈N•),∴n=1時,a1+a2=4a1+2,解得a2=5.
n≥2時,an+1=Sn+1-Sn=4an+2-(4an-1-2),
化為:an+1=4an-4an-1,變形為:an+1-2an=2(an-2an-1),∴bn=2bn-1.
∴{bn}是等比數列,公比為2,首項b1=a2-2a1=3.
(2)由(1)可得:bn=3×2n-1.
∴an+1-2an=3×2n-1.
∴$\frac{{a}_{n+1}}{{2}^{n+1}}$-$\frac{{a}_{n}}{{2}^{n}}$=$\frac{3}{4}$.
∴數列$\{\frac{{a}_{n}}{{2}^{n}}\}$是等差數列,首項為$\frac{1}{2}$,公差為$\frac{3}{4}$.
∴$\frac{{a}_{n}}{{2}^{n}}$=$\frac{1}{2}+\frac{3}{4}$(n-1),解得an=(3n-1)×2n-2.
∴cn=$\frac{{a}_{n}}{3n-1}$=2n-2,
$\frac{{c}_{n+1}}{{c}_{n}}$=$\frac{{2}^{n-1}}{{2}^{n-2}}$=2.
∴{cn}是等比數列,首項為$\frac{1}{2}$,公比為2.
點評 本題考查了數列遞推關系、等差數列與等比數列的通項公式,考查了推理能力與計算能力,屬于中檔題.


 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
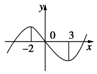 函數f(x)=x3+bx2+cx+d的圖象如圖,則函數g(x)=log${\;}_{\frac{1}{3}}$(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的單調遞增區間為( )
函數f(x)=x3+bx2+cx+d的圖象如圖,則函數g(x)=log${\;}_{\frac{1}{3}}$(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的單調遞增區間為( )| A. | [-2,+∞) | B. | (-∞,-2) | C. | (3,+∞) | D. | [3,+∞) |
查看答案和解析>>
科目:高中數學 來源:2017屆山東臨沭一中高三上學期10月月考數學(文)試卷(解析版) 題型:填空題
給定下列四個命題:
①若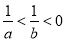 ,則
,則 ;
;
②已知直線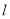 ,平面
,平面 ,
, 為不重合的兩個平面,若
為不重合的兩個平面,若 ,且
,且 ,則
,則 ;
;
③若 ,
, ,
, ,
, ,
, 成等比數列,則
成等比數列,則 ;
;
④設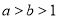 ,
, ,則
,則 .
.
其中真命題編號是 (寫出所有真命題的編號).
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2017屆江西吉安一中高三上學期段考一數學(文)試卷(解析版) 題型:解答題
已知動圓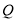 過定點
過定點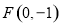 ,且與直線
,且與直線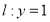 相切,橢圓
相切,橢圓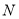 的對稱軸為坐標軸,
的對稱軸為坐標軸,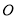 點為坐標原點,
點為坐標原點,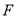 是其一個焦點,又點
是其一個焦點,又點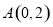 在橢圓
在橢圓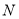 上.
上.
(1)求動圓圓心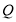 的軌跡
的軌跡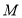 的標準方程和橢圓
的標準方程和橢圓 的標準方程;
的標準方程;
(2)若過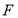 的動直線
的動直線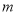 交橢圓
交橢圓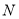 于
于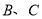 點,交軌跡
點,交軌跡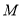 于
于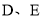 兩點,設
兩點,設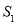 為
為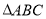 的面積,
的面積,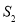 為
為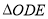 的面積,令
的面積,令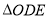 的面積,令
的面積,令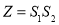 ,試求
,試求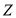 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com