
【題目】已知公比為正數的等比數列![]() ,首項
,首項![]() ,前n項和為
,前n項和為![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差數列.
成等差數列.
(Ⅰ)求數列![]() 的通項公式;
的通項公式;
(Ⅱ)設![]() ,求數列
,求數列![]() 的前n項和
的前n項和![]()
【答案】(Ⅰ)an=6×(![]() )n,(Ⅱ)Tn=2﹣(n+2)(
)n,(Ⅱ)Tn=2﹣(n+2)(![]() )n
)n
【解析】
(Ⅰ)設公比為q>0,由等比數列的通項公式和等差數列中項的性質,解方程可得q,即可得到所求通項公式;(Ⅱ)求得bn![]() n(
n(![]() )n,運用數列的求和方法:錯位相減法,結合等比數列的求和公式,化簡整理即可得到所求和.
)n,運用數列的求和方法:錯位相減法,結合等比數列的求和公式,化簡整理即可得到所求和.
(Ⅰ)an=6×(![]() )n,(Ⅱ)Tn=2﹣(n+2)(
)n,(Ⅱ)Tn=2﹣(n+2)(![]() )n
)n
依題意公比為正數的等比數列{an}(n∈N*),首項![]() =3,
=3,
設an=3qn﹣1,
∵![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列,
∴2(![]() )=
)=![]() +
+![]()
即2(![]() )=(
)=(![]() +(
+(![]() ),
),
化簡得4![]() =
=![]() ,
,
從而4q2=1,解得q=±![]() ,
,
∵{an}(n∈N*)公比為正數,
∴q![]() ,an=6×(
,an=6×(![]() )n,n∈N*;
)n,n∈N*;
(Ⅱ)bn![]() n(
n(![]() )n,
)n,
則Tn=1(![]() )+2(
)+2(![]() )2+3(
)2+3(![]() )3+…+(n﹣1)(
)3+…+(n﹣1)(![]() )n﹣1+n(
)n﹣1+n(![]() )n,
)n,
![]() Tn=1(
Tn=1(![]() )2+2(
)2+2(![]() )3+3(
)3+3(![]() )4+…+(n﹣1)(
)4+…+(n﹣1)(![]() )n+n(
)n+n(![]() )n+1,
)n+1,
兩式相減可得![]() Tn
Tn![]() (
(![]() )2+(
)2+(![]() )3+(
)3+(![]() )4+…+(
)4+…+(![]() )n﹣n(
)n﹣n(![]() )n+1
)n+1
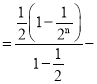 n(
n(![]() )n+1,
)n+1,
化簡可得Tn=2﹣(n+2)(![]() )n.
)n.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某廠家擬在新年舉行大型的促銷活動,經測算某產品當促銷費用為![]() 萬元時,銷售量
萬元時,銷售量![]() 萬件滿足
萬件滿足![]() (其中
(其中![]() ,
,![]() 為正常數).現假定生產量與銷售量相等,已知生產該產品
為正常數).現假定生產量與銷售量相等,已知生產該產品![]() 萬件還需投入成本
萬件還需投入成本![]() 萬元(不含促銷費用),產品的銷售價格定為
萬元(不含促銷費用),產品的銷售價格定為![]() 萬元/萬件.
萬元/萬件.
(1)將該產品的利潤![]() 萬元表示為促銷費用
萬元表示為促銷費用![]() 萬元的函數;
萬元的函數;
(2)促銷費用投入多少萬元時,廠家的利潤最大.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有3名男生、4名女生,在下列不同條件下,求不同的排列方法總數.
(1)選5人排成一排;
(2)排成前后兩排,前排4人,后排3人;
(3)全體排成一排,甲不站排頭也不站排尾;
(4)全體排成一排,女生必須站在一起;
(5)全體排成一排,男生互不相鄰.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小組共7人,利用假期參加義工活動,已知參加義工活動的次數為1,2,3的人數分別為2,2,3.現從這7人中隨機選出2人作為該組代表參加座談會:
(Ⅰ)設A為事件“選出的2人參加義工活動的次數之和為4”,求事件A發生的概率;
(Ⅱ)設X為選出的2人參加義工活動次數之差的絕對值,求隨機變量X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
:![]() ,
,![]() 為坐標原點,動點
為坐標原點,動點![]() 、
、![]() 在圓
在圓![]() 外,過點
外,過點![]() 、
、![]() 分別作圓
分別作圓![]() 的切線,切點分別為
的切線,切點分別為![]() 、
、![]() .
.
(1)若點![]() 在點
在點![]() 位置時,求此時切線
位置時,求此時切線![]() 的方程;
的方程;
(2)若點![]() 、
、![]() 滿足
滿足![]() ,
,![]() ,問直線
,問直線![]() :
:![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ?如果存在,求出點
?如果存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“割圓術”是劉徽最突出的數學成就之一,他在《九章算術注》中提出割圓術,并作為計算圓的周長,面積已經圓周率的基礎,劉徽把圓內接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個近似數值,這個結果是當時世界上圓周率計算的最精確數據.如圖,當分割到圓內接正六邊形時,某同學利用計算機隨機模擬法向圓內隨機投擲點,計算得出該點落在正六邊形內的頻率為0.8269,那么通過該實驗計算出來的圓周率近似值為(參考數據:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com