
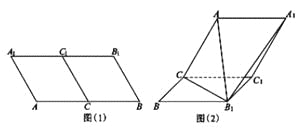
【題目】如圖(1),在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點.現把四邊形
的中點.現把四邊形![]() 沿
沿![]() 折起,如圖(2)所示,連結
折起,如圖(2)所示,連結![]() ,
,![]() ,
,![]() .
.
(1)求證:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
試題(1)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,可證
,可證![]() ,
,![]() 為正三角形,所以
為正三角形,所以![]() ,
,![]() ,由線面垂直的判定定理可知
,由線面垂直的判定定理可知![]() 平面
平面![]() ,從而證得
,從而證得![]() ;(2)根據勾股定理可證得
;(2)根據勾股定理可證得![]() ,所以
,所以![]() ,所以以
,所以以![]() 為原點,以
為原點,以![]() ,
,![]() ,
,![]() 為
為![]() ,
,![]() ,
,![]() 軸建立空間直角坐標系,分別求出平面
軸建立空間直角坐標系,分別求出平面![]() 的法向量,求出法向量的夾角,由于二面角
的法向量,求出法向量的夾角,由于二面角![]() 為鈍角,所以余弦值為負值.
為鈍角,所以余弦值為負值.
試題解析:(1)取![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,
,
∵在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,
∴![]() ,
,![]() 為正三角形,
為正三角形,
則![]() ,
,![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(2)∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點,
的中點,
∴![]() ,
,![]() ,
,![]() ,
,
若![]() ,
,
則![]() ,
,
則三角形![]() 為直角三角形,則
為直角三角形,則![]() ,
,
以![]() 為原點,以
為原點,以![]() ,
,![]() ,
,![]() 為
為![]() ,
,![]() ,
,![]() 軸建立空間直角坐標系,
軸建立空間直角坐標系,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
則![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則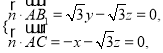 令
令![]() ,則
,則![]() ,
,![]() ,
,
則![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,則
,則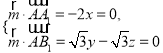 ,
,
令![]() ,則
,則![]() ,
,![]() ,即
,即![]() ,
,
則![]()
![]() ,
,
由于二面角![]() 是鈍二面角,
是鈍二面角,
∴二面角![]() 的余弦值是
的余弦值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線C1:![]() 和圓C2:(x-6)2+(y-1)2=1,過圓C2上一點P作圓的切線MN交拋物線C,于M,N兩點,若點P為MN的中點,則切線MN的斜率k>1時的直線方程為( )
和圓C2:(x-6)2+(y-1)2=1,過圓C2上一點P作圓的切線MN交拋物線C,于M,N兩點,若點P為MN的中點,則切線MN的斜率k>1時的直線方程為( )
A.4x-3y-22=0B.4x-3y-16=0C.2x-y-11+5=0D.4x-3y-26=0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,動點
,動點![]() ,線段QF與圓F相交于點P,線段PQ的長度與點Q到y軸的距離相等.
,線段QF與圓F相交于點P,線段PQ的長度與點Q到y軸的距離相等.
(Ⅰ)求動點Q的軌跡W的方程;
(Ⅱ)過點![]() 作兩條互相垂直的直線與W的交點分別是M和N(M在N的上方,A,M,N為不同的三點),求向量
作兩條互相垂直的直線與W的交點分別是M和N(M在N的上方,A,M,N為不同的三點),求向量![]() 在y軸正方向上的投影的取值范圍.
在y軸正方向上的投影的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車又稱為小黃車,近年來逐漸走進了人們的生活,也成為減少空氣污染,緩解城市交通壓力的一種重要手段.為調查某地區居民對共享單車的使用情況,從該地區居民中按年齡用隨機抽樣的方式隨機抽取了![]() 人進行問卷調查,得到這
人進行問卷調查,得到這![]() 人對共享單車的評價得分統計填入莖葉圖,如下所示(滿分
人對共享單車的評價得分統計填入莖葉圖,如下所示(滿分![]() 分):
分):

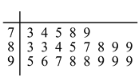
(1)找出居民問卷得分的眾數和中位數;
(2)請計算這![]() 位居民問卷的平均得分;
位居民問卷的平均得分;
(3)若在成績為![]() 分的居民中隨機抽取
分的居民中隨機抽取![]() 人,求恰有
人,求恰有![]() 人成績超過
人成績超過![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知中心在原點,焦點在![]() 軸上的橢圓的一個焦點為
軸上的橢圓的一個焦點為![]() ,
, 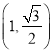 是橢圓上的一個點.
是橢圓上的一個點.
(1)求橢圓的標準方程;
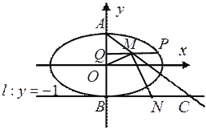
(2)設橢圓的上、下頂點分別為![]() ,
, ![]() (
(![]() )是橢圓上異于
)是橢圓上異于![]() 的任意一點,
的任意一點, ![]() 軸,
軸, ![]() 為垂足,
為垂足, ![]() 為線段
為線段![]() 中點,直線
中點,直線![]() 交直線
交直線![]() 于點
于點![]() ,
, ![]() 為線段
為線段![]() 的中點,如果
的中點,如果![]() 的面積為
的面積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】冠狀病毒是一個大型病毒家族,可引起感冒以及中東呼吸綜合征(MERS)和嚴重急性呼吸綜合征(SARS)等較嚴重疾病.出現的新型冠狀病毒(nCoV)是從未在人體中發現的冠狀病毒新毒株.人感染了新型冠狀病毒后常見體征有呼吸道癥狀、發熱、咳嗽、氣促和呼吸困難等.在較嚴重病例中,感染可導致肺炎、嚴重急性呼吸綜合征、腎衰竭,甚至死亡.某醫院為篩查冠狀病毒,需要檢測血液中的指標![]() .現從采集的血液樣品中抽取500份檢測指標
.現從采集的血液樣品中抽取500份檢測指標![]() 的值,由測量結果得下側頻率分布直方圖:
的值,由測量結果得下側頻率分布直方圖:

(1)求這500份血液樣品指標![]() 值的平均數
值的平均數![]() 和樣本方差
和樣本方差![]() (同一組數據用該區間的中點值作代表,記作
(同一組數據用該區間的中點值作代表,記作![]() );
);
(2)由頻率分布直方圖可以認為,這項指標![]() 的值X服從正態分布
的值X服從正態分布![]() ,其中
,其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .在統計學中,把發生概率小于3‰的事件稱為小概率事件(正常條件下小概率事件的發生是不正常的).該醫院非常關注本院醫生健康狀況,隨機抽取20名醫生,獨立的檢測血液中指標
.在統計學中,把發生概率小于3‰的事件稱為小概率事件(正常條件下小概率事件的發生是不正常的).該醫院非常關注本院醫生健康狀況,隨機抽取20名醫生,獨立的檢測血液中指標![]() 的值,結果發現4名醫生血液中指標
的值,結果發現4名醫生血液中指標![]() 的值大于正常值20.03,試根據題中條件判斷該院醫生的健康率是否正常,并說明理由.
的值大于正常值20.03,試根據題中條件判斷該院醫生的健康率是否正常,并說明理由.
附:參考數據與公式:![]() ,
,![]() ,
,![]() ;若
;若![]() ,則①
,則①![]() ;②
;②![]() ;③
;③![]() .
.![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市為了制定合理的節水方案,對居民用水情況進行調查,通過抽樣,獲得某年100為居民每人的月均用水量(單位:噸),將數據按照![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
(1)求直方圖的![]() 的值;
的值;
(2)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數,說明理由.
(3)估計居民月用水量的中位數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com