
【題目】已知函數![]() (其中e是自然對數的底數,a,
(其中e是自然對數的底數,a,![]() )在點
)在點![]() 處的切線方程是
處的切線方程是![]() .
.
(1)求函數![]() 的單調區間.
的單調區間.
(2)設函數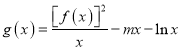 ,若
,若![]() 在
在![]() 上恒成立,求實數m的取值范圍.
上恒成立,求實數m的取值范圍.
【答案】(1)單調遞減區間為![]() ,單調遞增區間為
,單調遞增區間為![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() .由題意求出
.由題意求出![]() ,
,![]() ,即可求出
,即可求出![]() ,
,![]() ,代入
,代入![]() ,即可求出
,即可求出![]() 的單調區間;
的單調區間;
(2)由(1)知![]() .解法1:要使
.解法1:要使![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() 即可,利用導數求
即可,利用導數求![]() ;解法2:要使
;解法2:要使![]() 在
在![]() 上恒成立,等價于
上恒成立,等價于![]() 在
在![]() 上恒成立.令
上恒成立.令![]() ,則只需
,則只需![]() 即可,利用導數求
即可,利用導數求![]() ;解法3:要使
;解法3:要使![]() 在
在![]() 上恒成立,等價于
上恒成立,等價于![]() 在
在![]() 上恒成立. 先證明
上恒成立. 先證明![]() ,可得當
,可得當![]() 時,有
時,有![]() ,可得
,可得![]() ,即求實數m的取值范圍.
,即求實數m的取值范圍.
(1)對函數![]() 求導得
求導得![]() ,
,
由條件可知![]() ,
,![]() ,解得
,解得![]() ,
,![]() ,
,
所以![]() .
.
![]() .令
.令![]() 得
得![]() ,
,
于是,當![]() 時,
時,![]() ,函數
,函數![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,函數
,函數![]() 單調遞增.
單調遞增.
故函數![]() 的單調遞減區間為
的單調遞減區間為![]() ,單調遞增區間為
,單調遞增區間為![]() .
.
(2)由(1)知![]() .
.
解法1:要使![]() 在
在![]() 上恒成立,只需
上恒成立,只需![]() 即可.
即可.
因為![]() ,
,![]() ,
,
所以![]() 在
在![]() 上單調遞增.
上單調遞增.
因為當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
所以,![]() 在
在![]() 上存在唯一的零點
上存在唯一的零點![]() ,滿足
,滿足![]() ,
,
所以![]() ,
,
且![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
于是![]()
由![]() 得
得![]() ,此時必有
,此時必有![]() ,
,![]() ,
,
兩邊同時取自然對數,則有![]() ,即
,即![]() .
.
構造函數![]() (
(![]() ),則
),則![]() ,
,
所以函數![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() ,所以
,所以![]() ,即
,即![]() .
.
故![]() ,于是實數m的取值范圍是
,于是實數m的取值范圍是![]() .
.
解法2:要使![]() 在
在![]() 上恒成立,等價于
上恒成立,等價于![]() 在
在![]() 上恒成立.
上恒成立.
令![]() (
(![]() ),則只需
),則只需![]() 即可.
即可.
![]() ,令
,令![]() (
(![]() ),則
),則![]() ,
,
所以![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() ,
,![]() ,
,
所以![]() 有唯一的零點
有唯一的零點![]() ,且
,且![]() ,
,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
因為![]() ,兩邊同時取自然對數,則有
,兩邊同時取自然對數,則有![]() ,
,
即![]() .
.
構造函數![]() (
(![]() ),則
),則![]() ,
,
所以函數![]() 在
在![]() 上單調遞增,又
上單調遞增,又![]() ,
,
所以![]() ,即
,即![]() .
.
所以![]() .
.
于是實數m的取值范圍是![]()
解法3:要使![]() 在
在![]() 上恒成立,
上恒成立,
等價于![]() 在
在![]() 上恒成立.
上恒成立.
先證明![]() ,令
,令![]() (
(![]() ),則
),則![]() ,于是,當
,于是,當![]() 時,
時,![]() ,
,![]() 單調遞減;當
單調遞減;當![]() 時,
時,![]() ,
,![]() 單調遞增,所以
單調遞增,所以![]() ,故
,故![]() (當且僅當
(當且僅當![]() 時取等號)
時取等號)
所以,當![]() 時,有
時,有![]() ,所以
,所以![]() ,即
,即![]() ,當且僅當
,當且僅當![]() 時取等號,于是實數m的取值范圍是
時取等號,于是實數m的取值范圍是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某企業員工500人參加“學雷鋒”志愿活動,按年齡分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
區間 |
|
|
|
|
|
人數 | 50 | 50 | a | 150 | b |

(1)上表是年齡的頻數分布表,求正整數![]() 的值;
的值;
(2)現在要從年齡較小的第1,2,3組中用分層抽樣的方法抽取6人,年齡在第1,2,3組的人數分別是多少?
(3)在(2)的前提下,從這6人中隨機抽取2人參加社區宣傳交流活動,求至少有1人年齡在第3組的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應國家“精準扶貧、精準脫貧”的號召,某貧困縣在精準推進上下功夫,在精準扶貧上見實效.根據當地氣候特點大力發展中醫藥產業,藥用昆蟲的使用相應愈來愈多,每年春暖以后到寒冬前,昆蟲大量活動與繁殖,易于采取各種藥用昆蟲.已知一只藥用昆蟲的產卵數y(單位:個)與一定范圍內的溫度x(單位:℃)有關,于是科研人員在3月份的31天中隨機選取了5天進行研究,現收集了該種藥物昆蟲的5組觀察數據如表:
日期 | 2日 | 7日 | 15日 | 22日 | 30日 |
溫度 | 10 | 11 | 13 | 12 | 8 |
產卵數y/個 | 22 | 24 | 29 | 25 | 16 |
(1)從這5天中任選2天,記這2天藥用昆蟲的產卵數分別為m,n,求“事件m,n均不小于24”的概率?
(2)科研人員確定的研究方案是:先從這5組數據中任選2組,用剩下的3組數據建立線性回歸方程,再對被選取的2組數據進行檢驗.
①若選取的是3月2日與3月30日這2組數據,請根據3月7日、15日和22日這三組數據,求出y關于x的線性回歸方程?
②若由線性回歸方程得到的估計數據與所選出的檢驗數據的差的絕對值均不超過2個,則認為得到的線性回歸方程是可靠的,試問①中所得的線性回歸方程是否可靠?
附公式:![]() ,
,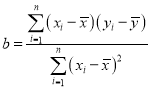
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】千百年來,我國勞動人民在生產實踐中根據云的形狀、走向、速度、厚度、顏色等的變化,總結了豐富的“看云識天氣”的經驗,并將這些經驗編成諺語,如“天上鉤鉤云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同學為了驗證“日落云里走,雨在半夜后”,觀察了所在地區A的100天日落和夜晚天氣,得到如下![]() 列聯表:
列聯表:
夜晚天氣 日落云里走 | 下雨 | 未下雨 |
出現 | 25 | 5 |
未出現 | 25 | 45 |
臨界值表 | ||||
P( | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
并計算得到![]() ,下列小波對地區A天氣判斷不正確的是( )
,下列小波對地區A天氣判斷不正確的是( )
A.夜晚下雨的概率約為![]()
B.未出現“日落云里走”夜晚下雨的概率約為![]()
C.有![]() 的把握認為“‘日落云里走’是否出現”與“當晚是否下雨”有關
的把握認為“‘日落云里走’是否出現”與“當晚是否下雨”有關
D.出現“日落云里走”,有![]() 的把握認為夜晚會下雨
的把握認為夜晚會下雨
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 在定義域
在定義域![]() 內的某個區間
內的某個區間![]() 上是增函數,且
上是增函數,且![]() 在
在![]() 上也是增函數,則稱
上也是增函數,則稱![]() 是
是![]() 上的“完美增函數”.已知
上的“完美增函數”.已知![]() ,
,![]() .
.
(1)判斷函數![]() 是否為區間
是否為區間![]() 上的“完美增函數”;
上的“完美增函數”;
(2)若函數![]() 是區間
是區間![]() 上的“完美增函數”,求實數
上的“完美增函數”,求實數![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() :
:![]() ,直線
,直線![]() :
:![]() .以極點
.以極點![]() 為原點,極軸為
為原點,極軸為![]() 軸的正半軸建立平面直角坐標系.
軸的正半軸建立平面直角坐標系.
(1)求直線![]() ,
,![]() 的直角坐標方程以及曲線
的直角坐標方程以及曲線![]() 的參數方程;
的參數方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,直線
兩點,直線![]() 與曲線C交于
與曲線C交于![]() ,
,![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com