分析:(1)正方形BB
1C
1C中,由Rt△BB
1E≌Rt△CBD證出B
1E⊥BD,由面面垂直的性質定理證出AE⊥平面BB
1C
1C,可得AE⊥BD,再由線面垂直判定定理即可證出BD⊥平面AB
1E;
(2)由AE⊥平面BB
1C
1C,可得∠AB
1E是直線AB
1與平面BB
1C
1C所成角.Rt△AB
1E中,算出AE、AB
1的長度,利用三角函數的定義算出sin∠AB
1E=
,即得直線AB
1與平面BB
1C
1C所成角的正弦值;
(3)算出S
△BCD=
S
BB1C1C=1,而AE⊥平面BCD,得三棱錐A-BCD的體積V
A-BCD=
S
△BCD•AE=
,從而可得三棱錐C-ABD的體積.
解答:解:(1)∵正方形BB
1C
1C中,D為CC
1中點,E為BC的中點
∴Rt△BB
1E≌Rt△CBD,可得∠CBD=∠BB
1E=90°-∠BEB
1因此∠BEB
1+∠CBD=90°,可得B
1E⊥BD
∵平面ABC⊥平面BB
1C
1C,平面ABC∩平面BB
1C
1C=BC,
正三角形ABC中,AE⊥BC
∴AE⊥平面BB
1C
1C,結合BD?平面BB
1C
1C,得AE⊥BD
∵AE、B
1E是平面AB
1E內的相交直線,∴BD⊥平面AB
1E;
(2)∵AE⊥平面BB
1C
1C,
∴BE是AB
1在平面BB
1C
1C內的射影,可得∠AB
1E是直線AB
1與平面BB
1C
1C所成角
∵正△ABC中,AE=
AB=
,正方形AA
1B
1B中,對角線AB
1=
AB=2
∴Rt△AB
1E中,sin∠AB
1E=
=
即直線AB
1與平面BB
1C
1C所成角的正弦值等于
;
(3)由前面的計算,可得S
△BCD=
S
BB1C1C=1
∵AE⊥平面BB
1C
1C,即AE⊥平面BCD
∴三棱錐A-BCD的體積V
A-BCD=
S
△BCD•AE=
×1×=
三棱錐C-ABD的體積為V
C-ABD=V
A-BCD=
.
點評:本題給出特殊正三棱柱,求證線面垂直并求直線與平面所成角和錐體的體積.著重考查了正棱柱的性質、線面垂直的判定與性質、直線與平面所成角的求法和錐體的體積公式等知識,屬于中檔題.

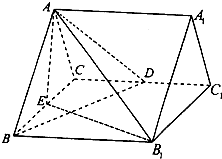 如圖,已知正三棱柱ABC-A1B1C1的所有棱長都為2,D為CC1中點,E為BC的中點.
如圖,已知正三棱柱ABC-A1B1C1的所有棱長都為2,D為CC1中點,E為BC的中點.

 如圖,已知正三棱柱ABC-A1B1C1各棱長都為a,P為線段A1B上的動點.
如圖,已知正三棱柱ABC-A1B1C1各棱長都為a,P為線段A1B上的動點. 如圖,已知正三棱柱ABC-A1B1C1的底面邊長為2cm,高位5cm,一質點自A點出發,沿著三棱柱的側面繞行兩周到達A1點的最短路線的長為
如圖,已知正三棱柱ABC-A1B1C1的底面邊長為2cm,高位5cm,一質點自A點出發,沿著三棱柱的側面繞行兩周到達A1點的最短路線的長為 如圖,已知正三棱柱ABC-A1B1C1的各條棱長都為a,P為A1B上的點.
如圖,已知正三棱柱ABC-A1B1C1的各條棱長都為a,P為A1B上的點. (2011•重慶三模)如圖,已知正三棱柱ABC-A1B1C1的所有棱長均為a,截面AB1C和A1BC1相交于DE,則三棱錐B-B1DE的體積為
(2011•重慶三模)如圖,已知正三棱柱ABC-A1B1C1的所有棱長均為a,截面AB1C和A1BC1相交于DE,則三棱錐B-B1DE的體積為