【題目】在平面直角坐標系xOy中，角α與角β均以Ox為始邊，它們的終邊關于y軸對稱，若sinα= 
，則cos（α﹣β）= ．
【答案】﹣ 
【解析】解：方法一：∵角α與角β均以Ox為始邊，它們的終邊關于y軸對稱，
∴sinα=sinβ= 
，cosα=﹣cosβ，
∴cos（α﹣β）=cosαcosβ+sinαsinβ=﹣cos2α+sin2α=2sin2α﹣1= 
﹣1=﹣
方法二：∵sinα= ，
當α在第一象限時，cosα= 
，
∵α，β角的終邊關于y軸對稱，
∴β在第二象限時，sinβ=sinα= ，cosβ=﹣cosα=﹣ ，
∴cos（α﹣β）=cosαcosβ+sinαsinβ=﹣ × + × =﹣
：∵sinα= ，
當α在第二象限時，cosα=﹣ ，
∵α，β角的終邊關于y軸對稱，
∴β在第一象限時，sinβ=sinα= ，cosβ=﹣cosα= ，
∴cos（α﹣β）=cosαcosβ+sinαsinβ=﹣ × + × =﹣
綜上所述cos（α﹣β）=﹣ ，
所以答案是：﹣
【考點精析】掌握同角三角函數基本關系的運用和兩角和與差的余弦公式是解答本題的根本，需要知道同角三角函數的基本關系：
；
;（3） 倒數關系：
；兩角和與差的余弦公式：
．
科目：高中數學 來源： 題型：
【題目】已知極點與直角坐標系的原點重合，極軸與x軸的正半軸重合，圓C的極坐標方程是ρ=asinθ，直線l的參數方程是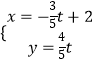 
（t為參數）
（1）若a=2，直線l與x軸的交點是M，N是圓C上一動點，求|MN|的最大值；
（2）直線l被圓C截得的弦長等于圓C的半徑的 
倍，求a的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某屆奧運會上，中國隊以26金18銀26銅的成績稱金牌榜第三、獎牌榜第二，某校體育愛好者在高三年級一班至六班進行了“本屆奧運會中國隊表現”的滿意度調查
結果只有“滿意”和“不滿意”兩種
，從被調查的學生中隨機抽取了50人，具體的調查結果如表：
班號 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
頻數 | 5 | 9 | 11 | 9 | 7 | 9 |
滿意人數 | 4 | 7 | 8 | 5 | 6 | 6 |
（1）在高三年級全體學生中隨機抽取一名學生，由以上統計數據估計該生持滿意態度的概率；
（2）若從一班至二班的調查對象中隨機選取4人進行追蹤調查，記選中的4人中對“本屆奧運會中國隊表現”不滿意的人數為
，求隨機變量的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點A（﹣1，0），B（1，0），C（0，1），直線y＝ax+b（a＞0）將△ABC分割為面積相等的兩部分，則b的取值范圍是（ ）
A.（0，1）B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】針對國家提出的延遲退休方案，某機構進行了網上調查，所有參與調查的人中，持“支持”、“保留”和“不支持”態度的人數如下表所示：
支持 | 保留 | 不支持 | |
|
|
|
|
|
|
|
|
(1)在所有參與調查的人中，用分層抽樣的方法抽取
個人，已知從持“不支持”態度的人中抽取了
人，求的值；
(2)在接受調查的人中，有
人給這項活動打出的分數如下：
，
，
，
，
，
，
，
，
，
，把這個人打出的分數看作一個總體，從中任取一個數，求該數與總體平均數之差的絕對值超過
的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如果定義在
上的函數
，對任意的
，都有
， 則稱該函數是“
函數”．
（I）分別判斷下列函數：①
；②
； ③
，是否為“函數”？（直接寫出結論）
（II）若函數
是“函數”，求實數
的取值范圍．
（III）已知
是“函數”，且在上單調遞增，求所有可能的集合
與
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
