
【題目】為了了解居民消費情況,某地區調查了10000戶小家庭的日常生活平均月消費金額,根據所得數據繪制了樣本頻率分布直方圖,如圖所示,每戶小家庭的平均月消費金額均不超過9千元,其中第六組第七組第八組尚未繪制完成,但是已知這三組的頻率依次成等差數列,且第六組戶數比第七組多500戶,
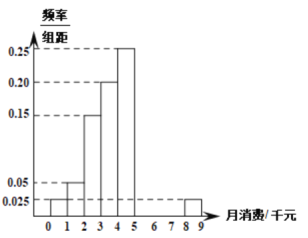
(1)求第六組第七組第八組的戶數,并補畫圖中所缺三組的直方圖;
(2)若定義月消費在3千元以下的小家庭為4類家庭,定義月消費在3千元至6千無的小家庭為B類家庭,定義月消費6千元以上的小家庭為C類家庭,現從這10000戶家庭中按分層抽樣的方法抽取80戶家庭召開座談會,間A,B,C各層抽取的戶數分別是多少?
【答案】(1)第六七八組的戶數分別是:1500戶1000戶500戶,直方圖見解析;(2)從A,B,C三類家庭分別抽取的戶數分別是18戶48戶14戶.
【解析】
(1)設第六七八組的戶數分別是x,y,z,再通過已知求出它們即得解,再求出第六七八組的小矩形高度,補充完整頻率分布直方圖;(2)求出A類家庭的頻率之和、B類家庭的頻率之和、C類家庭的頻率之和,即得解.
(1)設第六七八組的戶數分別是x,y,z,
它們的頻率之和為:![]() ,
,
所以這三組的戶數之和為:![]() .
.
由于這三組的頻率依次成等差數列,所以x,y,z也成等差數列,![]() ,
,
又![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() ,
,![]() .
.
所以第六七八組的小矩形高度分別為:![]() ,
,![]() ,
,![]() .
.
補直方圖(需注明第七組的小矩形高度為0.10,第六八兩組分別用虛線對應0.15和0.05.)
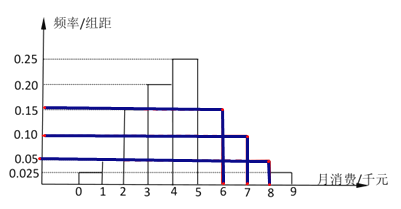
(2)A類家庭的頻率之和為:![]() ;
;
B類家庭的頻率之和為:![]() ;
;
C類家庭的頻率之和為:![]() .
.
故A,B,C類家庭分別抽取的戶數分別為:![]() ,
,![]() ,
,![]() .
.
答:(1)第六七八組的戶數分別是:1500戶1000戶500戶;
(2)從A,B,C三類家庭分別抽取的戶數分別是18戶48戶14戶.


科目:高中數學 來源: 題型:
【題目】南通風箏是江蘇傳統手工藝品之一.現用一張長2 m,寬1.5 m的長方形牛皮紙ABCD裁剪風箏面,裁剪方法如下:分別在邊AB,AD上取點E,F,將三角形AEF沿直線EF翻折到![]() 處,點
處,點![]() 落在牛皮紙上,沿
落在牛皮紙上,沿![]() ,
,![]() 裁剪并展開,得到風箏面
裁剪并展開,得到風箏面![]() ,如圖1.
,如圖1.
(1)若點E恰好與點B重合,且點![]() 在BD上,如圖2,求風箏面
在BD上,如圖2,求風箏面![]() 的面積;
的面積;
(2)當風箏面![]() 的面積為
的面積為![]() 時,求點
時,求點![]() 到AB距離的最大值.
到AB距離的最大值.
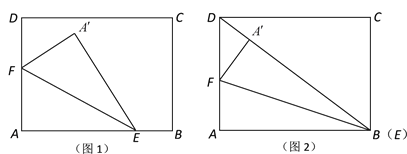
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一次高三年級統一考試中,數學試卷有一道滿分10分的選做題,學生可以從![]() ,
,![]() 兩道題目中任選一題作答.某校有900名高三學生參加了本次考試,為了了解該校學生解答該選做題的得分情況,計劃從900名考生的選做題成績中隨機抽取一個容量為10的樣本,為此將900名考生選做題的成績按照隨機順序依次編號為001一900.
兩道題目中任選一題作答.某校有900名高三學生參加了本次考試,為了了解該校學生解答該選做題的得分情況,計劃從900名考生的選做題成績中隨機抽取一個容量為10的樣本,為此將900名考生選做題的成績按照隨機順序依次編號為001一900.
(1)若采用隨機數表法抽樣,并按照以下隨機數表,以方框內的數字5為起點,從左向右依次讀取數據,每次讀取三位隨機數,一行讀數用完之后接下一行左端.寫出樣本編號的中位數;
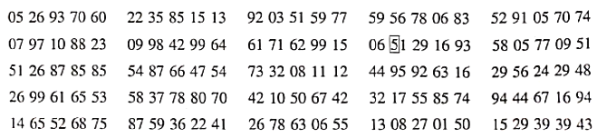
(2)若采用系統抽樣法抽樣,且樣本中最小編號為08,求樣本中所有編號之和:
(3)若采用分層軸樣,按照學生選擇![]() 題目或
題目或![]() 題目,將成績分為兩層,且樣本中
題目,將成績分為兩層,且樣本中![]() 題目的成績有8個,平均數為7,方差為4:樣本中
題目的成績有8個,平均數為7,方差為4:樣本中![]() 題目的成績有2個,平均數為8,方差為1.用樣本估計900名考生選做題得分的平均數與方差.
題目的成績有2個,平均數為8,方差為1.用樣本估計900名考生選做題得分的平均數與方差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區某農產品近幾年的產量統計如下表:

(1)根據表中數據,建立![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若近幾年該農產品每千克的價格![]() (單位:元)與年產量
(單位:元)與年產量![]() 滿足的函數關系式為
滿足的函數關系式為![]() ,且每年該農產品都能售完.
,且每年該農產品都能售完.
①根據(1)中所建立的回歸方程預測該地區![]() 年該農產品的產量;
年該農產品的產量;
②當![]() 為何值時,銷售額
為何值時,銷售額![]() 最大?
最大?
附:對于一組數據![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: 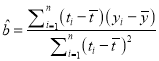 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).以原點
為參數).以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,且曲線
軸的正半軸為極軸建立極坐標系,且曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設直線![]() 上的定點
上的定點![]() 在曲線
在曲線![]() 外且其到
外且其到![]() 上的點的最短距離為
上的點的最短距離為![]() ,試求點
,試求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設點A是拋物線![]() 上到直線
上到直線![]() 的距離最短的點,點B是拋物線上異于點A的一點,直線AB與l交于P,過點P作y軸的平行線交拋物線于點C.
的距離最短的點,點B是拋物線上異于點A的一點,直線AB與l交于P,過點P作y軸的平行線交拋物線于點C.
(1)求點A的坐標;
(2)求證:直線BC過定點;
(3)求![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com