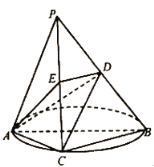
【題目】如圖，
是一個三棱錐，
是圓的直徑，
是圓上的點，
垂直圓所在的平面，
，
分別是棱
，的中點.
（1）求證：
平面
；
（2）若二面角
是
，
，求
與平面
所成角的正弦值.
【答案】（1）證明見解析；（2）
.
【解析】
（1）可證
，
，再利用
可得
，
，從而可證
平面
.
（2）可證
為二面角
的平面角，再以
為坐標原點，
，
，
方向分別為
軸，
軸，
軸的正方向，建立如圖所示的空間直角坐標系
. 求出平面
的法向量和直線
的方向向量后可求與平面所成角的正弦值.
（1）因為
是圓的直徑，所以.
因為
垂直圓所在的平面，且
在該平面中，所以.
因為
，
分別是棱
，的中點，
所以，所以，
又因為
，所以有平面.
（2）由（1）可知，
，
，
所以為二面角的平面角，
從而有
，則
.
又，
，得
.
以為坐標原點，，，方向分別為軸，軸，軸的正方向，建立如圖所示的空間直角坐標系.
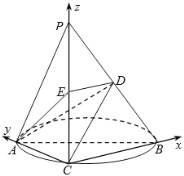
則
，
，
，
，
，
，
，
，
.
設
是平面的法向量，則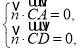
即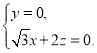
可取
.
故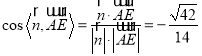
.
所以直線與平面所成角的正弦值為.
新課標快樂提優暑假作業陜西旅游出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目：高中數學 來源： 題型：
【題目】為了了解居民的家庭收人情況,某社區組織工作人員從該社區的居民中隨機抽取了
戶家庭進行問卷調查.經調查發現,這些家庭的月收人在
元到
元之間，根據統計數據作出如圖所示的頻率分布直方圖.已知圖中從左至右第一 、二、四小組的頻率之比為
,且第四小組的頻數為
.
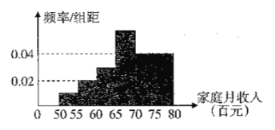
(1)求;
(2)求這戶家庭月收人的眾數與中位數(結果精確到
);
(3)這戶家庭月收入在第一、二、三小組的家庭中,用分層抽樣的方法任意抽取
戶家庭,并從這戶家庭中隨機抽取
戶家庭進行慰問,求這戶家庭月收入都不超過
元的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】幾位大學生響應國家的創業號召，開發了一款應用軟件，為激發大家的學習興趣，他們推出了“解數學題獲取軟件激活碼”的活動，這款軟件的激活碼為下列數學問題的答案：已知數列1、1、2、1、2、4、8、1、2、4、8、16、……，其中第一項是
，接下來的兩項是
，再接下來的三項是
，……，以此類推，求滿足如下條件的最小整數
且該數列的前
項和為2的整數冪，那么該軟件的激活碼是________。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知四邊形
為正方形，
平面，四邊形
與四邊形
也都為正方形，連接
，點
為
的中點，有下述四個結論：
①
； ②
與
所成角為
；
③
平面
； ④與平面
所成角為
．
其中所有正確結論的編號是（ ）
A.①②B.①②③C.①③④D.①②③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某創業團隊擬生產
兩種產品，根據市場預測，
產品的利潤與投資額成正比（如圖1），
產品的利潤與投資額的算術平方根成正比(如圖2).(注: 利潤與投資額的單位均為萬元)
（注：利潤與投資額的單位均為萬元）
(1)分別將兩種產品的利潤
、
表示為投資額
的函數；
(2)該團隊已籌集到10 萬元資金，并打算全部投入兩種產品的生產，問:當產品的投資額為多少萬元時，生產兩種產品能獲得最大利潤，最大利潤為多少?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
：
過點
，
為其焦點，過且不垂直于
軸的直線
交拋物線于
，
兩點，動點
滿足
的垂心為原點
.
（1）求拋物線的方程；
（2）求證：動點在定直線
上，并求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
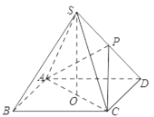
【題目】如圖，在四棱錐
中，已知四邊形
是邊長為
的正方形，點
在底面上的射影為底面的中心點
，點
在棱
上，且
的面積為1．
（1）若點是的中點，求證：平面
平面
；
（2）在棱上是否存在一點使得二面角
的余弦值為
？若存在，求出點的位置；若不存在，說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
