【題目】已知符號函數sgn（x）=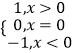 
，則函數f（x）=sgn（lnx）﹣lnx的零點個數為 ．
【答案】3
【解析】解：①如果lnx＞0，即x＞1時， 那么函數f（x）=sgn（lnx）﹣lnx轉化為函數f（x）=1﹣lnx，令1﹣lnx=0，得x=e，
即當x＞1時．函數f（x）=sgn（lnx）﹣lnx的零點是e；
②如果lnx=0，即x=1時，
那么函數f（x）=sgn（lnx）﹣lnx轉化為函數f（x）=0﹣lnx，令0﹣lnx=0，得x=1，
即當x=1時．函數f（x）=sgn（lnx）﹣lnx的零點是1；
③如果lnx＜0，即0＜x＜1時，
那么函數f（x）=sgn（lnx）﹣lnx轉化為函數f（x）=﹣1﹣lnx，令﹣1﹣lnx=0，x= 
，
即當0＜x＜1時．函數f（x）=sgn（lnx）﹣lnx的零點是 ；
綜上函數f（x）=sgn（lnx）﹣lnx的零點個數為3．
所以答案是：3．
新思維寒假作業系列答案科目：高中數學 來源： 題型：
【題目】如圖所示，游樂場中摩天輪勻速逆時針旋轉，每轉一圈需要6min，其中心距離地面40.5m，摩天輪的半徑為40m，已知摩天輪上點P的起始位置在最低點處，在時刻t（min）時點P距離地面的高度為f（t）=Asin（wt+φ）+h（A＞0，w＞0，﹣π＜φ＜0，t≥0）． 
（1）求f（t）的單調區間；
（2）求證：f（t）+f（t+2）+f（t+4）是定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】近幾年，電商行業的蓬勃發展也帶動了快遞業的高速發展.某快遞配送站每天至少要完成1800件包裹的配送任務，該配送站有8名新手快遞員和4名老快遞員，但每天最多安排10人進行配送.已知每個新手快遞員每天可配送240件包裹，日工資320元；每個老快遞員每天可配送300件包裹，日工資520元.
(Ⅰ)求該配送站每天需支付快遞員的總工資最小值；
(Ⅱ)該配送站規定:新手快遞員某個月被評為“優秀”，則其下個月的日工資比這個月提高12%.那么新手快遞員至少連續幾個月被評為“優秀”，日工資會超過老快遞員?
(參考數據: 
， 
， 
.)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高三年級在高校自主招生期間，把學生的平時成績按“百分制”折算并排序，選出前300名學生，并對這300名學生按成績分組，第一組[75，80），第二組[80，85），第三組[85，90），第四組[90，95），第五組[95，100]，如圖為頻率分布直方圖的一部分，其中第五組、第一組、第四組、第二組、第三組的人數依次成等差數列． （Ⅰ）請在圖中補全頻率分布直方圖；
（Ⅱ）若B大學決定在成績高的第4，5組中用
分層抽樣的方法抽取6名學生，并且分成2組，每組3人
進行面試，求95分（包括95分）以上的同學被分在同一個小組的概率．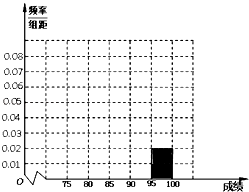
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線l1：2x+y+2=0，l2：mx+4y+n=0
（1）若l1⊥l2 ， 求m的值，；
（2）若l1∥l2 ， 且它們的距離為 
，求m、n的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】學校某研究性學習小組在對學生上課注意力集中情況的調查研究中，發現其在40分鐘的一節課中，注意力指數y與聽課時間x（單位：分鐘）之間的關系滿足如圖所示的圖象，當x∈（0，12]時，圖象是二次函數圖象的一部分，其中頂點A（10，80），過點B（12，78）；當x∈[12，40]時，圖象是線段BC，其中C（40，50）．根據專家研究，當注意力指數大于62時，學習效果最佳． 
（1）試求y=f（x）的函數關系式；
（2）教師在什么時段內安排內核心內容，能使得學生學習效果最佳？請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓E： 
的左、右焦點分別為F1、F2 ， 離心率 
，P為橢圓E上的任意一點（不含長軸端點），且△PF1F2面積的最大值為1．
（1）求橢圓E的方程；
（2）已知直x﹣y+m=0與橢圓E交于不同的兩點A，B，且線AB的中點不在圓 
內，求m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C：x2+y2﹣2x﹣2ay+a2﹣24=0（a∈R）的圓心在直線2x﹣y=0上．
（1）求實數a的值；
（2）求圓C與直線l：（2m+1）x+（m+1）y﹣7m﹣4=0（m∈R）相交弦長的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，定義在[﹣1，5]上的函數f（x）由一段線段和拋物線的一部分組成． （Ⅰ）求函數f（x）的解析式；
（Ⅱ）指出函數f（x）的自變量x在什么范圍內取值時，函數值大于0，小于0或等于0（不需說理由）．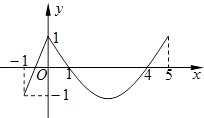
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com