
【題目】已知橢圓![]() 的一個焦點為
的一個焦點為![]() ,離心率為
,離心率為![]() .不過原點的直線
.不過原點的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,設(shè)直線
兩點,設(shè)直線![]() ,直線
,直線![]() ,直線
,直線![]() 的斜率分別為
的斜率分別為![]() ,且
,且![]() 成等比數(shù)列.
成等比數(shù)列.
(1)求![]() 的值;
的值;
(2)若點![]() 在橢圓
在橢圓![]() 上,滿足
上,滿足![]() 的直線
的直線![]() 是否存在?若存在,求出直線
是否存在?若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】分析:(1)由離心率公式及基本量運算可得![]() ,從而得方程;設(shè)直線
,從而得方程;設(shè)直線![]() 的方程為
的方程為![]() ,由
,由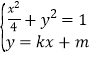 ,得
,得![]() ,由已知
,由已知![]() ,利用韋達定理帶入可得
,利用韋達定理帶入可得![]() ;
;
(2)假設(shè)存在直線![]() 滿足題設(shè)條件,且設(shè)
滿足題設(shè)條件,且設(shè)![]() ,由
,由![]() ,得
,得![]() ,代入橢圓方程得:
,代入橢圓方程得:![]() ,整理得
,整理得![]() ,由韋達定理帶入可得
,由韋達定理帶入可得![]() ,可知直線不存在.
,可知直線不存在.
詳解:(1)由已知得![]() ,則
,則![]() ,
,
故橢圓![]() 的方程為
的方程為![]() ;
;
設(shè)直線![]() 的方程為
的方程為![]() ,
,
由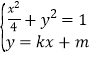 ,得
,得![]() ,
,
則![]() ,
,
由已知![]() ,
,
則![]() ,即
,即![]() ,
,
所以![]() ;
;
(2)假設(shè)存在直線![]() 滿足題設(shè)條件,且設(shè)
滿足題設(shè)條件,且設(shè)![]() ,
,
由![]() ,得
,得![]() ,
,
代入橢圓方程得:![]() ,
,
即![]() ,
,
則![]() ,即
,即![]() ,
,
則![]() ,
,
所以![]() ,
,
化簡得:![]() ,而
,而![]() ,則
,則![]() ,
,
此時,點![]() 中有一點在橢圓的上頂點(或下頂點處),與
中有一點在橢圓的上頂點(或下頂點處),與![]() 成等比數(shù)列相矛盾,故這樣的直線不存在.
成等比數(shù)列相矛盾,故這樣的直線不存在.


科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 在
在![]() 上的單調(diào)遞增區(qū)間;
上的單調(diào)遞增區(qū)間;
(2)將函數(shù)![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度,再將圖象上所有點的橫坐標伸長到原來的
個單位長度,再將圖象上所有點的橫坐標伸長到原來的![]() 倍(縱坐標不變),得到函數(shù)
倍(縱坐標不變),得到函數(shù)![]() 的圖象.求證:存在無窮多個互不相同的整數(shù)
的圖象.求證:存在無窮多個互不相同的整數(shù)![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】密碼學是一種密寫技術(shù),即把信息寫成代碼的技術(shù),將信息轉(zhuǎn)換成保密語言的過程叫編碼,有保密形式語言道出原始信息的過程稱作譯碼.凱撒(![]() 公元前100-前44年)曾使用過一種密碼系統(tǒng),現(xiàn)稱為凱撒暗碼,按照這種系統(tǒng)的規(guī)則,原始信息的字母都用另一字母代替,后者在標準字母表中的位置比前者靠后三位(即暗碼
公元前100-前44年)曾使用過一種密碼系統(tǒng),現(xiàn)稱為凱撒暗碼,按照這種系統(tǒng)的規(guī)則,原始信息的字母都用另一字母代替,后者在標準字母表中的位置比前者靠后三位(即暗碼![]() 原碼后移3個位置).如:標準字母表:
原碼后移3個位置).如:標準字母表:![]() ,凱撒暗碼表:
,凱撒暗碼表:![]() ,這樣就將信息“JuliusCaesar”編碼為“MxolxvFdhvdu”當你知道所得到的信息使用凱撒暗碼編寫成的密碼時,譯碼工作很容易,只需把上述過程倒過來進行.當然現(xiàn)在的密寫技術(shù)要復雜許多,這里我構(gòu)造一種編碼技術(shù),請同學根據(jù)編碼過程自己破譯一下:信息字母與編碼后暗語字母的對應(yīng)法則是:暗碼
,這樣就將信息“JuliusCaesar”編碼為“MxolxvFdhvdu”當你知道所得到的信息使用凱撒暗碼編寫成的密碼時,譯碼工作很容易,只需把上述過程倒過來進行.當然現(xiàn)在的密寫技術(shù)要復雜許多,這里我構(gòu)造一種編碼技術(shù),請同學根據(jù)編碼過程自己破譯一下:信息字母與編碼后暗語字母的對應(yīng)法則是:暗碼![]() 原碼后移
原碼后移![]() 后得到的字母(
后得到的字母(![]() 為原碼字母在語句中的位置即第幾個字母,若移出字母表則在后面續(xù)一張字母表,其中[]為取整符號,空格不計數(shù)).那么若一句話的暗碼為“JnrzjPKNI”,其原碼是__________.
為原碼字母在語句中的位置即第幾個字母,若移出字母表則在后面續(xù)一張字母表,其中[]為取整符號,空格不計數(shù)).那么若一句話的暗碼為“JnrzjPKNI”,其原碼是__________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某廠生產(chǎn)某種產(chǎn)品的年固定成本為250萬元,每生產(chǎn)![]() 千件,需另投入成本
千件,需另投入成本![]() ,當年產(chǎn)量不足80千件時,
,當年產(chǎn)量不足80千件時,![]() (萬元);當年產(chǎn)量不小于80千件時,
(萬元);當年產(chǎn)量不小于80千件時,![]() (萬元),每件售價為0.05萬元,通過市場分析,該廠生產(chǎn)的商品能全部售完.
(萬元),每件售價為0.05萬元,通過市場分析,該廠生產(chǎn)的商品能全部售完.
(1)寫出年利潤![]() (萬元)關(guān)于年產(chǎn)量
(萬元)關(guān)于年產(chǎn)量![]() (千件)的函數(shù)解析式;
(千件)的函數(shù)解析式;
(2)年產(chǎn)量為多少千件時,該廠在這一商品的生產(chǎn)中所獲利潤最大?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】解答下列各題:
(1)已知扇形的周長為10cm,面積為4cm2,求扇形圓心角的弧度數(shù).
(2)已知一扇形的圓心角是72°,半徑等于20cm,求扇形的面積.
(3)已知一扇形的周長為40cm,求它的半徑和圓心角取什么值時,才能使扇形的面積最大?最大面積是多少?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=4cosωxsin(ωx![]() )(ω>0)的最小正周期是π.
)(ω>0)的最小正周期是π.
(1)求函數(shù)f(x)在區(qū)間(0,π)上的單調(diào)遞增區(qū)間;
(2)若f(x0)![]() ,x0∈[
,x0∈[![]() ,
,![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)函數(shù)f(x)=tan(ωx+φ)(ω>0,0<φ<![]() ),已知函數(shù)y=f(x)的圖象與x軸相鄰兩個交點的距離為
),已知函數(shù)y=f(x)的圖象與x軸相鄰兩個交點的距離為![]() ,且圖象關(guān)于點M(-
,且圖象關(guān)于點M(-![]() ,0)對稱.
,0)對稱.
(1)求f(x)的解析式;
(2)求f(x)的單調(diào)區(qū)間;
(3)求不等式-1≤f(x)≤![]() 的解集.
的解集.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)據(jù)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的平均值為2,方差為1,則數(shù)據(jù)
的平均值為2,方差為1,則數(shù)據(jù)![]() ,
,![]() ,
,![]() ,
,![]() 相對于原數(shù)據(jù)( )
相對于原數(shù)據(jù)( )
A.一樣穩(wěn)定B.變得比較穩(wěn)定C.變得比較不穩(wěn)定D.穩(wěn)定性不可以判斷
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】改革開放以來,人們的支付方式發(fā)生了巨大轉(zhuǎn)變.近年來,移動支付已成為主要支付方式之一.為了解某校學生上個月A,B兩種移動支付方式的使用情況,從全校所有的1000名學生中隨機抽取了100人,發(fā)現(xiàn)樣本中A,B兩種支付方式都不使用的有5人,樣本中僅使用A和僅使用B的學生的支付金額分布情況如下:
支付方式 | 不大于2000元 | 大于2000元 |
僅使用A | 27人 | 3人 |
僅使用B | 24人 | 1人 |
(Ⅰ)估計該校學生中上個月A,B兩種支付方式都使用的人數(shù);
(Ⅱ)從樣本僅使用B的學生中隨機抽取1人,求該學生上個月支付金額大于2000元的概率;
(Ⅲ)已知上個月樣本學生的支付方式在本月沒有變化.現(xiàn)從樣本僅使用B的學生中隨機抽查1人,發(fā)現(xiàn)他本月的支付金額大于2000元.結(jié)合(Ⅱ)的結(jié)果,能否認為樣本僅使用B的學生中本月支付金額大于2000元的人數(shù)有變化?說明理由.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com