
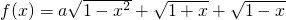 的最大值為g(a).
的最大值為g(a).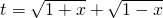 ,求t的取值范圍;
,求t的取值范圍; +
+ ,
, ∈[2,4],t≥0.
∈[2,4],t≥0. ,2].
,2]. =
= t2-1
t2-1 t2-1)+t=
t2-1)+t= at2+t-a,(
at2+t-a,( ≤t≤2)
≤t≤2) at2+t-a在t∈[
at2+t-a在t∈[ ,2]的最大值,
,2]的最大值, 是拋物線M(t)的對稱軸,分別分以下情況討論.
是拋物線M(t)的對稱軸,分別分以下情況討論. ,2]上單調遞增,∴g(a)=M(2)=a+2.
,2]上單調遞增,∴g(a)=M(2)=a+2. ,2),∴g(a)=2;
,2),∴g(a)=2; ,2]圖象開口向下;
,2]圖象開口向下; ∈(0,
∈(0, ],即a≤-
],即a≤- 時,則g(a)=M(
時,則g(a)=M( )=
)= ;
; ∈(
∈( ,2]即-
,2]即- <a≤-
<a≤- 時,則g(a)=M(-
時,則g(a)=M(- )=-a-
)=-a- ;
; ∈(2,+∞),-
∈(2,+∞),- <a<0時,則g(a)=M(2)=a+2.
<a<0時,則g(a)=M(2)=a+2.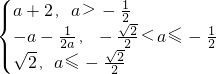 .
. 時,g(a)=a+2是增函數,值域為(
時,g(a)=a+2是增函數,值域為( ,+∞);
,+∞);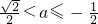 時,g(a)=-a-
時,g(a)=-a- 是增函數,g(a)的值域為(
是增函數,g(a)的值域為( ,
, ];
]; 時,g(a)=
時,g(a)= 是常函數,g(a)的值域為{
是常函數,g(a)的值域為{ }.
}.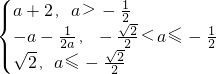 的最小值為
的最小值為 ,無最大值.
,無最大值. =
= t2-1即可求出m(t),g(a)即為函數M(t)=
t2-1即可求出m(t),g(a)即為函數M(t)= at2+t-a在t∈[
at2+t-a在t∈[ ,2]的最大值;然后再結合二次函數在閉區間上的最值求法分對稱軸和區間的三種位置關系分別討論即可.(注意開口方向)
,2]的最大值;然后再結合二次函數在閉區間上的最值求法分對稱軸和區間的三種位置關系分別討論即可.(注意開口方向) 時,g(a)=a+2是增函數,值域為(
時,g(a)=a+2是增函數,值域為( ,+∞);②當-
,+∞);②當-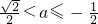 時,g(a)=-a-
時,g(a)=-a- 是增函數,g(a)的值域為(
是增函數,g(a)的值域為( ,
, ];③當a
];③當a 時,g(a)=
時,g(a)= 是常函數,g(a)的值域為{
是常函數,g(a)的值域為{ }.由此能求出g(a)的單調性和最值.
}.由此能求出g(a)的單調性和最值.

科目:高中數學 來源:2012-2013學年安徽省巢湖市無為中學高一(上)期中數學試卷(解析版) 題型:解答題
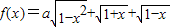 的最大值為g(a).
的最大值為g(a).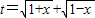 ,求t的取值范圍;
,求t的取值范圍;查看答案和解析>>
科目:高中數學 來源:2012-2013學年安徽省巢湖市無為中學高一(上)期中數學試卷(解析版) 題型:解答題
 的最大值為g(a).
的最大值為g(a).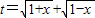 ,求t的取值范圍;
,求t的取值范圍;查看答案和解析>>
科目:高中數學 來源:2010-2011學年重慶市萬州二中高一(上)期中數學試卷(解析版) 題型:解答題
 的最大值為g(a).
的最大值為g(a).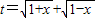 ,求t的取值范圍;
,求t的取值范圍;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com