
【題目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)記 ,設
,設![]() ,
, ![]() 為函數
為函數![]() 圖象上的兩點,且
圖象上的兩點,且![]() .
.
(i)當![]() 時,若
時,若![]() 在
在![]() ,
, ![]() 處的切線相互垂直,求證:
處的切線相互垂直,求證: ![]() ;
;
(ii)若在點![]() ,
, ![]() 處的切線重合,求
處的切線重合,求![]() 的取值范圍.
的取值范圍.
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)先求函數導數,轉化為研究導函數零點,即方程![]() =0的根的情況,當
=0的根的情況,當![]() ,導函數不變號,在
,導函數不變號,在![]() 上單調遞減,當
上單調遞減,當![]() 時,有兩個不等根,列表分析導函數符號變化規律,確定對應單調區間,(2)(i)利用導數幾何意義化簡條件:
時,有兩個不等根,列表分析導函數符號變化規律,確定對應單調區間,(2)(i)利用導數幾何意義化簡條件: ![]() 在
在![]() ,
, ![]() 處的切線相互垂直,得
處的切線相互垂直,得![]() ,利用基本不等式證明不等式,(ii)先分別求出切線方程,再根據切線重合得
,利用基本不等式證明不等式,(ii)先分別求出切線方程,再根據切線重合得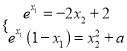 ,消元
,消元![]() 得
得![]() ,利用導數研究函數
,利用導數研究函數![]() ,
, ![]() 單調性,確定函數
單調性,確定函數![]() 值域,進而確定
值域,進而確定![]() 的取值范圍.
的取值范圍.
試題解析:解:(1)![]() ,則
,則![]() ,
,
當![]() 即
即![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上單調遞減,
上單調遞減,
當![]() 時即
時即![]() 時,
時, ![]() ,
,
此時![]() 在
在![]() 和
和![]() 上都是單調遞減的,在
上都是單調遞減的,在![]() 上是單調遞增的;
上是單調遞增的;
(2)(i)![]() ,據題意有
,據題意有![]() ,又
,又![]() ,
,
則![]() 且
且![]() ,
, ![]() ,
,
法1: ![]() ,
,
當且僅當![]() 即
即![]() ,
, ![]() 時取等號.
時取等號.
法2: ![]() ,
, 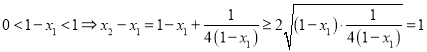 ,
,
當且僅當![]() 時取等號.
時取等號.
(ii)要在點![]() 處的切線重合,首先需要在點
處的切線重合,首先需要在點![]() 處的切線的斜率相等,
處的切線的斜率相等,
而![]() 時,
時, ![]() ,則必有
,則必有![]() ,即
,即![]() ,
, ![]() ,
,
![]() 處的切線方程是:
處的切線方程是: ![]()
![]() 處的切線方程是:
處的切線方程是: ![]() ,
,
即![]() ,
,
據題意則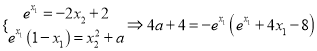 ,
, ![]() ,
,
設![]() ,
, ![]() ,
, ![]() ,
,
設![]() ,
, ![]() 在
在![]() 上恒成立,
上恒成立,
則![]() 在
在![]() 上單調遞增
上單調遞增![]() ,
,
則![]() ,
, ![]() 在
在![]() 上單調遞增,
上單調遞增,
則![]() ,再設
,再設![]() ,
, ![]() ,
,
![]() ,
, ![]() 在
在![]() 上單調遞增,
上單調遞增, ![]() ,
,
則![]() 在
在![]() 恒成立,
恒成立,
即當![]() 時,
時, ![]() 的值域是
的值域是![]() ,
,
故![]() ,即為所求.
,即為所求.


科目:高中數學 來源: 題型:
【題目】如圖,隔河看兩目標A、B,但不能到達,在岸邊選取相距 ![]() km的C、D兩點,并測得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面內),求兩目標A、B之間的距離.
km的C、D兩點,并測得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A、B、C、D在同一平面內),求兩目標A、B之間的距離. 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 為圓
為圓![]() 的直徑,點
的直徑,點![]() ,
, ![]() 在圓
在圓![]() 上,
上, ![]() ,矩形
,矩形![]() 和圓
和圓![]() 所在的平面互相垂直,已知
所在的平面互相垂直,已知![]() ,
, ![]() .
.
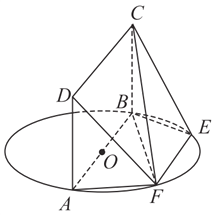
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直線![]() 與平面
與平面![]() 所成角的大小;
所成角的大小;
(Ⅲ)當![]() 的長為何值時,二面角
的長為何值時,二面角![]() 的大小為
的大小為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=2BC=4,E為邊AB的中點,將△ADE沿直線DE翻轉成△A1DE.若M為線段A1C的中點,則在△ADE翻轉過程中: ①|BM|是定值;
②點M在圓上運動;
③一定存在某個位置,使DE⊥A1C;
④一定存在某個位置,使MB∥平面A1DE.
其中正確的命題是( )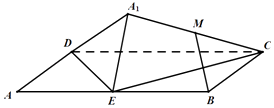
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(sinx+cosx)2+2cos2x﹣2.
(1)求函數f(x)的最小正周期及單調遞增區間;
(2)當x∈[ ![]() ,
, ![]() ]時,求函數f(x)的值域.
]時,求函數f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x+1)的定義域是[﹣1,3],則y=f(x2)的定義域是( )
A.[0,4]
B.[0,16]
C.[﹣2,2]
D.[1,4]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知隨機變量X服從正態分布N(μ,σ2),且P(μ﹣2σ<X≤μ+2σ)=0.9544,P(μ﹣σ<X≤μ+σ)=0.6826,若μ=4,σ=1,則P(5<X<6)=( )
A.0.1358
B.0.1359
C.0.2716
D.0.2718
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com