
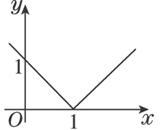
(1)y=|x-1|;
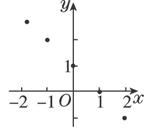
(2)y=1-x,x∈Z;
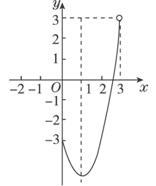
(3)y=2x2-4x-3,0≤x<3;
(4)y=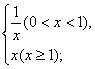
(5)y=|x+1|+|x-2|;
(6)y=|x2-x|.
思路解析:對(1)、(5)、(6)先去掉絕對值符號再畫圖象.對(2)、(3)注意定義域對函數的影響;對(4)要分段來畫.
解:(1)由y=|x-1|,討論去掉絕對值得y=![]()
其圖象如下圖所示.
(2)∵函數的定義域為{x|x∈Z}.
∴函數圖象由一些點組成,這些點都在直線y=1-x上,這些點稱為整點.(如下圖)
(3)∵0≤x<3,
∴這個函數的圖象是拋物線y=2x2-4x-3介于0≤x<3之間一段,如下圖所示.
(4)這個函數的圖象由兩部分組成.
當0<x<1時,為雙曲線y=![]() 的一段; 當x≥1時,為直線y=x的一段.
的一段; 當x≥1時,為直線y=x的一段.

(5)將原函數解析式中的絕對值去掉,化為分段函數.
f(x)=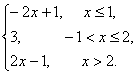
其圖象如圖所示.
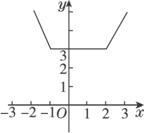
(6)先作y=x2-x的圖象,如圖,.
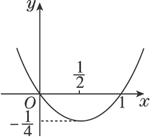
再作y=|x2-x|的圖象,如圖
要點提示
(1)函數的圖象不一定是一條或幾條無限長的平滑曲線,也可以是一些點,一些線段,一段曲線等.
(2)對含有絕對值的函數,可先根據絕對值的定義去掉絕對值符號,再畫圖象,如例(1)、例(5).畫形如y=|f(x)|的函數圖象,還可以先畫出y=f(x)的圖象,再把x軸下方的圖象關于x軸作對稱圖形,如例(6).
(3)應掌握一些基本函數的圖象畫法,如一次函數、二次函數,反比例函數,常數函數等.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com