
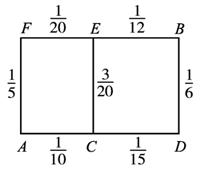
(1)請你為其選擇一條由A到B的路線,使得途中發生堵車事件的概率最小;
(2)若記路線A→C→F→B中遇到堵車次數為隨機變量ξ,求ξ的數學期望.
解析:(1)記路段MN不發生堵車事件為![]() ,因為各路段發生堵車事件都是獨立的,且在同一路段發生堵車事件最多只有一次.
,因為各路段發生堵車事件都是獨立的,且在同一路段發生堵車事件最多只有一次.
所以路線A→C→D→B中遇到堵車的概率為P1為1-P(![]() )=1-P(
)=1-P(![]() )·P(
)·P(![]() )·P(
)·P(![]() )=1-[1-P(AC)][1-P(CD)][1-P(DB)]=1-
)=1-[1-P(AC)][1-P(CD)][1-P(DB)]=1-![]() ;
;
同理路線A→C→F→B中遇到堵車的概率P2=1-P(![]() )=
)=![]() (小于
(小于![]() );
);
路線A→E→F→B中遇到堵車的概率為P3=1-P(![]() )=
)=![]() (大于
(大于![]() );
);
顯然要使得由A到B的路線途中發生堵車事件的概率最小,只可能在以上三條路線中選擇,因此選擇路線A→C→F→B可使得途中堵車事件的概率最小.
(2)路線A→C→F→B中遇到堵車次數ξ可取值為0,1,2,3,P(ξ=0)=P(![]() )=
)=![]() ;
;
P(ξ=1)=P(![]() )+P(
)+P(![]() )+P(
)+P(![]() )=
)=![]() ;
;
P(ξ=2)=P(AC·CF·![]() )+P(AC·
)+P(AC·![]() ·FB)+P(
·FB)+P(![]() ·CF·FB)=
·CF·FB)=
![]() ;
;
P(ξ=3)=P(AC·CF·FB)
=![]()
∴Eξ=0·![]() .
.
答:路線A→C→F→B中遇到堵車次數的數學期望為![]() .
.


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
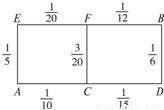
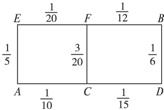 某先生居住在城鎮的A處,準備開車到單位B處上班,若該地各路段發生堵車事件都是獨立的,且在同一路段發生堵車事件最多只有一次,發生堵車事件的概率如如圖所示.(例如:A→C→D算作兩個路段:路段AC發生堵車事件的概率為
某先生居住在城鎮的A處,準備開車到單位B處上班,若該地各路段發生堵車事件都是獨立的,且在同一路段發生堵車事件最多只有一次,發生堵車事件的概率如如圖所示.(例如:A→C→D算作兩個路段:路段AC發生堵車事件的概率為| 1 |
| 10 |
| 1 |
| 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 某先生居住在城鎮的A處,準備開車到單位B處上班,若該地各路段發生堵車事件都是獨立的,且在同一路段發生堵車事件最多只有一次,發生堵車事件的概率,如圖.( 例如:A→C→D算作兩個路段:路段AC發生堵車事件的概率為
某先生居住在城鎮的A處,準備開車到單位B處上班,若該地各路段發生堵車事件都是獨立的,且在同一路段發生堵車事件最多只有一次,發生堵車事件的概率,如圖.( 例如:A→C→D算作兩個路段:路段AC發生堵車事件的概率為| 1 |
| 10 |
| 1 |
| 15 |
查看答案和解析>>
科目:高中數學 來源:2012年蘇教版高數選修2-3 2.1隨機變量概率分布二項分布練習卷(解析版) 題型:解答題
某先生居住在城鎮的A處,準備開車到單位B處上班,若該地各路段發生堵車事件都是獨立的,且在同一路段發生堵車事件最多只有一次,發生堵車事件的概率如圖所示.(例如:A→C→D算作兩個路段:路段AC發生堵車事件的概率為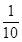 ,路段CD發生堵車事件的概率為115).
,路段CD發生堵車事件的概率為115).
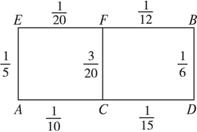
(1)請你為其選擇一條由A到B的路線,使得途中發生堵車事件的概率最小;
(2)若記路線A→C→F→B中遇到堵車次數為隨機變量X,求X的概率分布.
查看答案和解析>>
科目:高中數學 來源:《2.1-2.2 隨機變量及其概率分布、二項分布》2011年同步練習(解析版) 題型:解答題
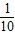 ,路段CD發生堵車事件的概率為
,路段CD發生堵車事件的概率為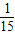 ).
).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com