已知定圓C1和兩定點M、N,圓心C1不在MN的中垂線上,過MN作圓C2與圓C1交于P、Q兩點,求證:PQ必過一定點.
【答案】
分析:建立直角坐標系,得到圓C
1的方程和兩定點M、N的坐標,C
2在MN的中垂線上,設出C
2的坐標(0,k),
寫出圓C
2的方程,將兩圓的方程相減便得到公共弦PQ的方程,再利用直線系過定點得到定點坐標.
解答: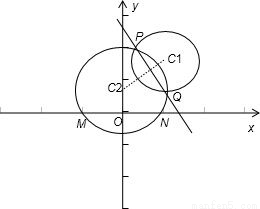
證明:以MN所在的直線為x軸,以其中垂線為 y軸,
建立直角坐標系,如圖:設M(-m,0)、N(m,0),C
2(0,k),
設定圓C
1 的方程為 (x-a)
2+(y-b)
2=r
2,
圓C
2的方程為 x
2+(y-k)
2=k
2+m
2,
由題意知,a、b、r、m為定值,k為 參數.
將兩圓的方程相減得直線PQ的方程為-2ax+(2k-2b)y+a
2+b
2+m
2-r
2=0,
即2ky+(-2ax-2by+a
2+b
2+m
2-r
2)=0,
由

,
得
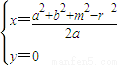
,
∴直線PQ經過定點(
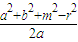
,0).
點評:本題考查兩圓的位置關系以及直線和圓的位置關系,兩圓相交時,將兩圓的方程相減即得公共弦所在的直線方程,直線λ(ax+by+c)+(mx+ny+p)=0經過兩直線ax+by+c=0與 mx+ny+p=0的交點.

 證明:以MN所在的直線為x軸,以其中垂線為 y軸,
證明:以MN所在的直線為x軸,以其中垂線為 y軸, ,
,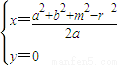 ,
,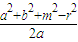 ,0).
,0).

 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案