【題目】已知數列{an}的前n項和為Sn ， 且 
，數列{bn}滿足 
，則數列{anbn}的前n項和Tn= ．
【答案】10+（3n﹣5）2n+1
【解析】解：由已知得，當n≥2時，an=Sn﹣Sn﹣1=（ 
n2﹣ 
n）﹣[ （n﹣1）2﹣ （n﹣1）]=3n﹣2，又a1=1=3×1﹣2，符合上式．
故數列{an}的通項公式an=3n﹣2．
又因為 
，
所以log2bn= 
（an+2）=n，即bn=2n ，
令cn=anbn ．
則cn=（3n﹣2）2n ．
所以Tn=1×21+422+723+…+（3n﹣2）2n ， ①
2Tn=1×22+4×23+724+…+（3n﹣2）2n+1 ， ②
由②﹣①得：﹣Tn=2+322+323+…+（3n﹣5）2n+1=3×（2+22+…+2n）﹣（3n﹣2）2n+1﹣2
=﹣（3n﹣5）2n+1﹣10，
所以Tn=10+（3n﹣5）2n+1
故答案是：10+（3n﹣5）2n+1 ．
【考點精析】本題主要考查了數列的前n項和的相關知識點，需要掌握數列{an}的前n項和sn與通項an的關系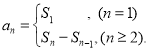
才能正確解答此題．
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
其中P，M是非空數集，且P∩M=，設f（P）={y|y=f（x），x∈P}，f（M）={y|y=f（x），x∈M}．
（I）若P=（﹣∞，0），M=[0，4]，求f（P）∪f（M）；
（II）是否存在實數a＞﹣3，使得P∪M=[﹣3，a]，且f（P）∪f（M）=[﹣3，2a﹣3]？若存在，請求出滿足條件的實數a；若不存在，請說明理由；
（III）若P∪M=R，且0∈M，I∈P，f（x）是單調遞增函數，求集合P，M．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于不等式
，則對區間
上的任意x都成立的實數t的取值范圍是_______．
【答案】
【解析】
根據二次函數的單調性求出x2﹣3x+2在區間[0，2]上的最小值和最大值，把問題轉化關于t的不等式組
得答案．
∵x2﹣3x+2=
，
∴當x∈[0，2]時，
，（x2﹣3x+2）max=2．
∴
．
∴對于不等式
（2t﹣t2）≤x2﹣3x+2≤3﹣t2，對區間[0，2]上任意x都成立的實數t的取值范圍是[﹣1，1﹣
]．
故答案為：[﹣1，1﹣].
【點睛】
本題考查函數恒成立問題，考查了不等式的解法，體現了數學轉化思想方法，是基礎題．二次不等式分含參二次不等式和不含參二次不等式；對于含參的二次不等式問題，先判斷二次項系數是否含參，接著討論參數等于0，不等于0，再看式子能否因式分解，若能夠因式分解則進行分解，再比較兩根大小,結合圖像得到不等式的解集.
【題型】填空題
【結束】
16
【題目】等差數列{an}的公差d≠0滿足
成等比數列，若
=1，Sn是{
}的前n項和，則
的最小值為________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】曲線C1的參數方程為
(θ為參數),將曲線C1上所有點的橫坐標伸長為原來的2倍,縱坐標伸長為原來的
倍,得到曲線C2.以平面直角坐標系xOy的原點O為極點,x軸的正半軸為極軸,取相同的單位長度建立極坐標系,已知直線l:ρ(cosθ-2sinθ)=6.
(1)求曲線C2和直線l的普通方程.
(2)P為曲線C2上任意一點,求點P到直線l的距離的最值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從1至9這9個自然數中任取兩個：
恰有一個偶數和恰有一個奇數；
至少有一個是奇數和兩個數都是奇數；
至多有一個奇數和兩個數都是奇數；
至少有一個奇數和至少有一個偶數．
在上述事件中，是對立事件的是
A. B. 
C. D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義在R上的函數f（x），滿足 
，且f（3）=f（1）﹣1．
（1）求實數k的值；
（2）若函數g（x）=f（x）+f（﹣x）（﹣2≤x≤2），求g（x）的值域．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用長為18 cm的鋼條圍成一個長方體形狀的框架，要求長方體的長與寬之比為2：1，問該長方體的長、寬、高各為多少時，其體積最大？最大體積是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知：函數
，當x∈（－3，2）時，
>0，當x∈（－
，－3）
（2，+）時，<0
（I）求a，b的值；
（II）若不等式
的解集為R，求實數c的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
