
P、Q、M、N四點都在橢圓x2+![]() =1上,F為橢圓在y軸正半軸上的焦點.已知
=1上,F為橢圓在y軸正半軸上的焦點.已知![]() 與
與![]() 共線,
共線,![]() 與
與![]() 共線,且
共線,且![]() ?
?![]() =0.求四邊形PMQN的面積的最小值和最大值。
=0.求四邊形PMQN的面積的最小值和最大值。
本小題主要考查橢圓和直線的方程與性質,兩條直線垂直的條件,兩點間的距離,不等式的性質等基本知識及綜合分析能力。
解:如圖,由條件知MN和PQ是橢圓的兩條弦,相交于焦點F(0,1),且PQ⊥MN,直線PQ、MN中至少有一條存在斜率,不妨設PQ的斜率為k,又PQ過點F(0,1),
故PQ方程為y=kx+1
將此式代入橢圓方程得
(2+k2)x2+2kx-1=0
設P、Q兩點的坐標分別為(x1,y1),(x2,y2),則
![]()
從而 |PQ|2=(x1-x2)2+(y1-y2)2
=![]()
亦即 |PQ|=![]()
(i)當k≠0時,MN的斜率為![]() ,同上可推得
,同上可推得
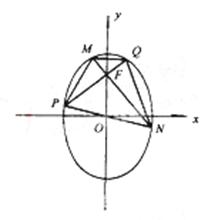
|MN|=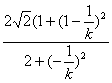
故四邊形面積
S=![]() |PQ|?|MN|
|PQ|?|MN|
=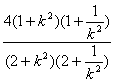
= 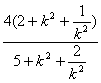
令![]() ,得
,得
![]()
因為 ![]()
當![]() 時,u=2,S=
時,u=2,S=![]() ,
,
且S是以u為自變量的增函數,
所以![]()
(ii)當k=0時,MN為橢圓長軸,|MN|=![]() ,|PQ|=
,|PQ|=![]() ,
,
S=![]() |PQ|?|MN|=2.
|PQ|?|MN|=2.
綜合(i),(ii)知,四邊形PMQN面積的最大值為2,最小值為![]() 。
。


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| y2 |
| 2 |
| PF |
| FQ |
| MF |
| FN |
| PF |
| MF |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 2 |
| PF |
| FQ |
| MF |
| FN |
| PF |
| MF |
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 2 |
| PF |
| FQ |
| MF |
| FN |
| PF |
| MF |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2011-2012學年大綱版高三上學期單元測試(8)數學試卷 題型:解答題
(本小題滿分12分)
P、Q、M、N四點都在橢圓 上,F為橢圓在y軸正半軸上的焦點.已知
上,F為橢圓在y軸正半軸上的焦點.已知 與
與 共
共
線,且 與
與 共線.求四邊形PMQN的面積的最小值和最大值.
共線.求四邊形PMQN的面積的最小值和最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com