日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

【題目】在四棱錐中，平面，四邊形是矩形，，，分別是棱，，的中點.

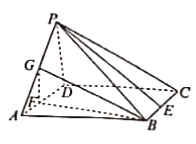
（1）求證：平面；

（2）若，，求點到平面的距離.

【答案】(1)證明見解析；(2)

【解析】

（1）連接，證明平面平面，即可說明平面；

（2）先計算出，再利用等體積法，即可求出點到平面的距離.

（1）證明：連接，∵在矩形中，，分別是，中點，

∴，，∴四邊形是平行四邊形，∴.

∵是的中點，∴.

∵平面，平面，

∴平面，平面.

∵，∴平面平面.

∵平面，∴平面.

（2）解：法一：∵平面，，∴平面.

過在平面內，作，垂足為，則.

∵，∴平面，∴長是點到平面的距離.

在矩形中，是中點，，，.

∴.

∵，，∴，

即點到平面的距離為.

法二：設到平面的距離為，

在矩形中，，，∴.

∵平面，平面，∴，

∵，∴，，

∴的面積為.

∵的面積為，，

∴，∴，即點到平面的距離為.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

【題目】某媒體對“男女延遲退休″這一公眾關注的問題進行名意調查，如表是在某單位得到的數據：

贊同

反對

合計

男

50

150

200

女

30

170

200

合計

80

320

400

（I）能否有97.5%的把握認為對這一問題的看法與性別有關？

（II）從贊同“男女延遲退休”的80人中，利用分層抽樣的方法抽出8人，然后從中選出3人進行陳述發言，設發言的女士人數為X，求X的分布列和期望．

參考公式：

0.10

0.05

0.025

0.010

0.005

0.001

2.706

3.841

5.024

6.635

7.879

10.828

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】f(x)是定義在區間[-c,c]上的奇函數,其圖象如下圖所示.令g(x)=af(x)+b,則下列關于函數g(x)的結論:

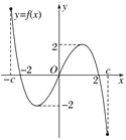
①若a<0,則函數g(x)的圖象關于原點對稱;

②若a=-1,-2<b<0,則方程g(x)=0有大于2的實根;

③若a≠0,b=2,則方程g(x)=0有兩個實根;

④若a≠0,b=2,則方程g(x)=0有三個實根.

其中,正確的結論為________.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知數列{an}的前n項和Sn＝pn＋q(p≠0且p≠1)，求證：數列{an}為等比數列的充要條件為q＝－1.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】為了調查民眾對國家實行“新農村建設”政策的態度，現通過網絡問卷隨機調查了年齡在20周歲至80周歲的100人，他們年齡頻數分布和支持“新農村建設”人數如下表：

年齡

頻數

10

20

30

20

10

10

支持“新農村建設”

3

11

26

12

6

2

（1）根據上述統計數據填下面的列聯表，并判斷是否有的把握認為以50歲為分界點對“新農村建設”政策的支持度有差異；

年齡低于50歲的人數

年齡不低于50歲的人數

合計

支持

不支持

合計

（2）為了進一步推動“新農村建設”政策的實施，中央電視臺某節目對此進行了專題報道，并在節目最后利用隨機撥號的形式在全國范圍內選出4名幸運觀眾（假設年齡均在20周歲至80周歲內），給予適當的獎勵.若以頻率估計概率，記選出4名幸運觀眾中支持“新農村建設”人數為，試求隨機變量的分布列和數學期望.

參考數據：

0.150

0.100

0.050

0.025

0.010

0.005

0.001

2.072

2.706

3.841

5.024

6.635

7.879

10.828

參考公式：，其中.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知．

（1）當時，求不等式的解集;

（2）若時，不等式恒成立，求a的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知直線的參數方程為為參數），以坐標原點為極點，軸的正半軸為極軸建立極坐標系，曲線的極坐標方程為.

（1）求直線的普通方程和曲線的直角坐標方程；

（2）設點，直線與曲線交于兩點，求的值.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f（x）＝alnx﹣3x在x處取得極值．

（1）若對任意x∈（0，+∞），f（x）≤m恒成立，求實數m的取值范圍；

（2）討論函數F（x）＝f（x）+x2+k（k∈R）的零點個數．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】某班級有3名同學報名參加學校組織的辯論賽，現有甲、乙兩個辨題可以選擇，學校決定讓選手以抽取卡片（除上面標的數不同外其他完全相同）的方式選擇辯題，且每名選手抽取后放回．已知共有10張卡片，卡片上分別標有共10個數．若抽到卡片上的數為質數（2，3，5，7），則選擇甲辨題，否則選擇乙辯題．

（1）求這3名同學中至少有1人選擇甲辨題的概率．

（2）用X、Y分別表示這3名同學中選擇甲、乙辨題的人數，求的分布列和數學期望．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 青青av在线 | 日韩精品在线一区 | 四虎影视最新网址 | 久久精品亚洲 | 性处破╳╳╳高清欧美 | 欧美一级一级一级 | 亚洲一区在线影院 | 欧美日韩网站在线观看 | 日韩三级在线 | 亚洲精品一区二区三区四区高清 | 久久涩涩 | 午夜激情福利电影 | 国产精选一区二区 | 亚洲精品成人在线 | 国产高清不卡一区 | 欧美久久一区 | 国产片侵犯亲女视频播放 | 午夜a级理论片915影院 | 国产女人高潮视频在线观看 | 亚洲精品视频在线 | 伊人超碰在线 | 欧美成人精品一区二区三区 | 日本视频一区二区三区 | 日本精品免费 | 青春草在线观看 | 亚洲h视频在线观看 | 久久午夜激情 | 国产精品一线二线在线观看 | 欧美精品在欧美一区二区少妇 | 精品久久久久久久久久久 | 精品国产乱码久久久久夜 | 亚洲免费观看 | k8久久久一区二区三区 | 男女免费在线观看 | 狠狠av| 国产区第一页 | 日韩高清中文字幕 | 久草ab| 激情综合久久 | 毛片网站在线 | 国产传媒毛片精品视频第一次 |