【題目】某射擊運動員每次擊中目標的概率是
，在某次訓練中，他只有4發子彈，并向某一目標射擊.
（1）若4發子彈全打光，求他擊中目標次數
的數學期望；
（2）若他擊中目標或子彈打光就停止射擊，求消耗的子彈數
的分布列.
科目：高中數學 來源： 題型：
【題目】為了響應黨的十九大所提出的教育教學改革，某校啟動了數學教學方法的探索,學校將髙一年級部分生源情況基本相同的學生分成甲、乙兩個班，每班40人，甲班按原有傳統模式教學，乙班實施自主學習模式.經過一年的教學實驗，將甲、乙兩個班學生一年來的數學成績取平均數，兩個班學生的平均成績均在[50，100]，按照區間[50，60），[60,70)，[70,80），[80，90)，[90,100]進行分組,繪制成如下頻率分布直方圖，規定不低于80分(百分制）為優秀，
，
(I)完成表格,并判斷是否有90%以上的把握認為“數學成績優秀與教學改革有關”
〔Ⅱ）從乙班[70,80），[80，90)，[90,100]分數段中,按分層抽樣隨機抽取7名學生座談，
從中選三位同學發言,記來自[80，90)發言的人數為隨機變量x，求x的分布列和期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有甲、乙兩個游戲項目，要參與游戲，均需每次先付費
元（不返還），游戲甲有
種結果：可能獲得
元，可能獲得元，可能獲得
元，這三種情況的概率分別為
，
，
；游戲乙有
種結果：可能獲得
元，可能獲得
元，這兩種情況的概率均為.
（1）某人花元參與游戲甲兩次，用
表示該人參加游戲甲的收益（收益=參與游戲獲得錢數-付費錢數），求的概率分布及期望；
（2）用
表示某人參加
次游戲乙的收益，為任意正整數，求證：的期望為.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著人們生活水平的不斷提高，家庭理財越來越引起人們的重視.某一調查機構隨機調查了5個家庭的月收入與月理財支出（單位：元）的情況，如下表所示：
月收入 | 8 | 10 | 9 | 7 | 11 |
月理財支出 |
|
|
|
|
|
（I）在下面的坐標系中畫出這5組數據的散點圖；
（II）根據上表提供的數據，用最小二乘法求出
關于
的線性回歸方程
；
（III）根據（II）的結果，預測當一個家庭的月收入為
元時，月理財支出大約是多少元？
（附：回歸直線方程中，
，
.）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=（2﹣a）（x﹣1）﹣2lnx，（a∈R）． （Ⅰ）當a=1時，求f（x）的單調區間；
（Ⅱ）若函數f（x）在（0， 
）上無零點，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在如圖所示的多面體中，
平面
，
平面，
，且
，
是
的中點．
（
）求證：
．
（
）若
為線段
上一點，且
，求證：
平面
．
（
）在棱
上是否存在一點
，使得直線
與平面所成的角為
．若存在，指出點的位置；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在數列
中，已知
，且對于任意正整數n都有
．
（1）令
，求數列
的通項公式；
（2）求的通項公式；
（3）設
是一個正數，無論為何值，都有一個正整數
使
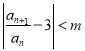成立．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若數列{
}的前n項和Sn=2-2．
（1）求數列{}的通項公式；
（2）若bn=log
，Sn=b1+b2+…+bn，對任意正整數n，Sn+（n+m）
＜0恒成立，試求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于正整數集合
，如果去掉其中任意一個元素
之后，剩余的所有元素組成的集合都能分為兩個交集為空集的集合，且這兩個集合的所有元素之和相等，就稱集合
為“和諧集”．
（
）判斷集合
是否是“和諧集”（不必寫過程）．
（
）請寫出一個只含有
個元素的“和諧集”，并證明此集合為“和諧集”．
（
）當
時，集合
，求證：集合不是“和諧集”．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
