
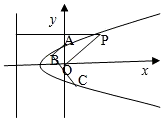
 已知向量n=(1,0),點A(0,2),動點P滿足:|
已知向量n=(1,0),點A(0,2),動點P滿足:|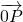 |比向量
|比向量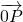 在n的方向上的投影多2.
在n的方向上的投影多2.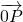 在n的方向上的投影為|
在n的方向上的投影為|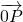 |cos∠POx,即P點到y軸的距離,又|
|cos∠POx,即P點到y軸的距離,又|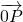 |比向量
|比向量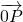 在n的方向上的投影多2,
在n的方向上的投影多2, y12-1,y1),C(
y12-1,y1),C( y22-1,y2),
y22-1,y2), =(
=( y12-1,y1-2)=
y12-1,y1-2)= ( y1-2)(y1+2,4),
( y1-2)(y1+2,4), =(
=( y22-
y22- y12,y2-y1)=
y12,y2-y1)= ( y2-y1) (y2+y1,4),
( y2-y1) (y2+y1,4), •
• =0,即
=0,即 ( y1-2)
( y1-2) ( y2-y1)[(y1+2)(y2+y1)+16]=0,
( y2-y1)[(y1+2)(y2+y1)+16]=0,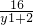 -y1=2-(
-y1=2-(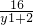 +y1+2).由均值不等式得y2≥10或y2≤-6.
+y1+2).由均值不等式得y2≥10或y2≤-6.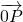 在n的方向上的投影為|
在n的方向上的投影為|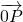 |cos∠POx,即P點到y軸的距離,又|
|cos∠POx,即P點到y軸的距離,又|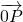 |比向量
|比向量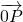 在n的方向上的投影多2,得出P點到原點的距離等于它到直線x=-2的距離,最后根據拋物線的定義得出所求的軌跡方程;
在n的方向上的投影多2,得出P點到原點的距離等于它到直線x=-2的距離,最后根據拋物線的定義得出所求的軌跡方程;

科目:高中數學 來源: 題型:
 已知向量n=(1,0),點A(0,2),動點P滿足:|
已知向量n=(1,0),點A(0,2),動點P滿足:|| 0P |
| 0P |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中數學 來源:2009年湖北省武漢市硚口區高三數學交流試卷1(文理合卷)(解析版) 題型:解答題
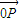 |比向量
|比向量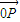 在n的方向上的投影多2.
在n的方向上的投影多2.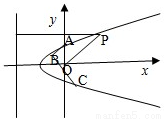
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com