
| A. | 4 | B. | 2 | C. | $\frac{4}{5}$ | D. | $\frac{1}{2}$ |
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
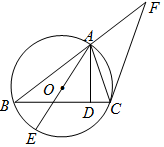 如圖,已知圓O是△ABC的外接圓,AB=BC,AD是 BC邊上的高,AE 是圓O的直徑,過點C作圓O的切線交BA的延長線于點F.
如圖,已知圓O是△ABC的外接圓,AB=BC,AD是 BC邊上的高,AE 是圓O的直徑,過點C作圓O的切線交BA的延長線于點F.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖所示,有一塊矩形空地ABCD,AB=2km,BC=4km,根據周邊環境及地形實際,當地政府規劃在該空地內建一個箏形商業區AEFG,箏形的頂點A,E,F,G為商業區的四個入口,其中入口F在邊BC上(不包含頂點),入口E,G分別在邊AB,AD上,且滿足點A,F恰好關于直線EG對稱,矩形內箏形外的區域均為綠化區.
如圖所示,有一塊矩形空地ABCD,AB=2km,BC=4km,根據周邊環境及地形實際,當地政府規劃在該空地內建一個箏形商業區AEFG,箏形的頂點A,E,F,G為商業區的四個入口,其中入口F在邊BC上(不包含頂點),入口E,G分別在邊AB,AD上,且滿足點A,F恰好關于直線EG對稱,矩形內箏形外的區域均為綠化區.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com