
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)是否存在實數![]() ,使得至少有一個
,使得至少有一個![]() ,使
,使![]() 成立,若存在,求出實數
成立,若存在,求出實數![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
【答案】(1)單調遞增區間為![]() 和
和![]() ,單調減區間為
,單調減區間為![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】試題分析: ![]() 求得函數f(x)的定義域,求導函數,對a討論,利用導數的正負,即可確定函數f(x)的單調區間;
求得函數f(x)的定義域,求導函數,對a討論,利用導數的正負,即可確定函數f(x)的單調區間;
(2)先考慮“至少有一個![]() ,使
,使![]() 成立”的否定“
成立”的否定“![]() ,
, ![]() 恒成立”.即可轉化為a+(a+1)xlnx≥0恒成立,令φ(x)=a+(a+1)xlnx,則只需φ(x)≥0在x∈(0,+∞)恒成立即可.
恒成立”.即可轉化為a+(a+1)xlnx≥0恒成立,令φ(x)=a+(a+1)xlnx,則只需φ(x)≥0在x∈(0,+∞)恒成立即可.
試題解析:
(1)函數![]() 的定義域為
的定義域為![]() ,
, ![]()
1)當![]() 時,由
時,由![]() 得,
得, ![]() 或
或![]() ,由
,由![]() 得
得![]() ,
,
故函數![]() 的單調遞增區間為
的單調遞增區間為![]() 和
和![]() ,單調減區間為
,單調減區間為![]()
2)當![]() 時,
時, ![]() ,
, ![]() 的單調增區間為
的單調增區間為![]()
(2)先考慮“至少有一個![]() ,使
,使![]() 成立”的否定“
成立”的否定“![]() ,
, ![]() 恒成立”.
恒成立”.
即可轉化為![]() 恒成立.
恒成立.
令![]() ,則只需
,則只需![]() 在
在![]() 恒成立即可,
恒成立即可,
![]() ,
,
當![]() 時,在
時,在![]() 時,
時, ![]() ,在
,在![]() 時,
時, ![]()
![]() 的最小值為
的最小值為![]() ,由
,由![]() 得
得![]() ,
,
故當![]() 時,
時, ![]() 恒成立,
恒成立,
當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 不能恒成立,
不能恒成立,
當![]() 時,取
時,取![]() ,有
,有![]() ,
, ![]() 在
在![]() 不能恒成立,
不能恒成立,
綜上所述,即![]() 時,至少有一個
時,至少有一個![]() ,使
,使![]() 成立.
成立.


科目:高中數學 來源: 題型:
【題目】(題文)某研究小組在電腦上進行人工降雨模擬實驗,準備用A、B、C三種人工降雨方式分別對甲、乙、丙三地實施人工降雨,其實驗數據統計如下:
方式 | 實施地點 | 大雨 | 中雨 | 小雨 | 模擬實驗總次數 |
A | 甲 | 4次 | 6次 | 2次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定對甲、乙、丙三地實施的人工降雨彼此互不影響,請你根據人工降雨模擬實驗的統計數據:
(1)求甲、乙、丙三地都恰為中雨的概率;
(2)考慮到旱情和水土流失,如果甲地恰需中雨即達到理想狀態,乙地必須是大雨才達到理想狀態,丙地只要是小雨或中雨即達到理想狀態,記“甲、乙、丙三地中達到理想狀態的個數”為隨機變量ξ,求隨機變量ξ的分布列和均值E(ξ).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l方程為(m+2)x-(m+1)y-3m-7=0,m∈R.
(Ⅰ)求證:直線l恒過定點P,并求出定點P的坐標;
(Ⅱ)若直線l在x軸,y軸上的截距相等,求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi,yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為![]() ,則下列結論中不正確的是( )
,則下列結論中不正確的是( )
A. 若該大學某女生身高為170cm,則可斷定其體重必為![]()
B. 回歸直線過樣本點的中心![]()
C. 若該大學某女生身高增加1cm,則其體重約增加![]()
D. y與x具有正的線性相關關系
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某印刷廠為了研究單冊書籍的成本![]() (單位:元)與印刷冊數
(單位:元)與印刷冊數![]() (單位:千冊)之間的關系,在印制某種書籍時進行了統計,相關數據見下表:
(單位:千冊)之間的關系,在印制某種書籍時進行了統計,相關數據見下表:
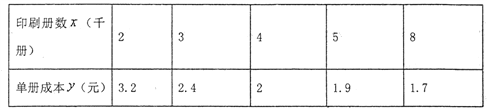
根據以上數據,技術人員分別借助甲、乙兩種不同的回歸模型,得到兩個回歸方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)為了評價兩種模型的擬合效果,完成以下任務.
①完成下表(計算結果精確到0.1);
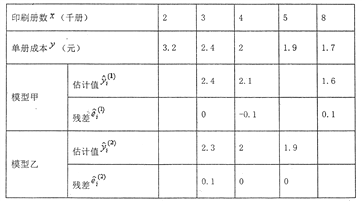
②分別計算模型甲與模型乙的殘差平方和![]() 及
及![]() ,并通過比較
,并通過比較![]() 的大小,判斷哪個模型擬合效果更好.
的大小,判斷哪個模型擬合效果更好.
(2)該書上市之后,受到廣大讀者熱烈歡迎,不久便全部售罄,于是印刷廠決定進行二次印刷,根據市場調查,新需求量為10千冊,若印刷廠以每冊5元的價格將書籍出售給訂貨商,求印刷廠二次印刷10千冊獲得的利潤?(按(1)中擬合效果較好的模型計算印刷單冊書的成本).
查看答案和解析>>
科目:高中數學 來源: 題型:
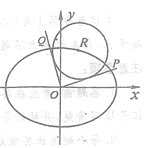
【題目】如圖,在平面直角坐標系![]() 中,已知
中,已知![]() 是橢圓
是橢圓![]() 上的一點,從原點
上的一點,從原點![]() 向圓
向圓![]() 作兩條切線,分別交橢圓于點
作兩條切線,分別交橢圓于點![]() .
.
(1)若![]() 點在第一象限,且直線
點在第一象限,且直線![]() 互相垂直,求圓
互相垂直,求圓![]() 的方程;
的方程;
(2)若直線![]() 的斜率存在,并記為
的斜率存在,并記為![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解學生參加體育活動的情況,學校對學生進行隨機抽樣調查,其中一個問題是“你平均每天參加體育活動的時間是多少?”,共有4個選項:A,1.5小時以上,B,1-1.5小時,C,0.5-1小時,D,0.5小時以下.圖(1),(2)是根據調查結果繪制的兩幅不完整的統計圖,請你根據統計圖提供的信息,解答以下問題:
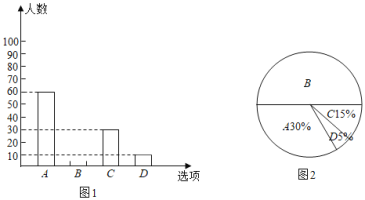
(1)本次一共調查了多少名學生.
(2)在圖(1)中將![]() 對應的部分補充完整.
對應的部分補充完整.
(3)若該校有3000名學生,你估計全校有多少名學生平均每天參加體育活動的時間在0.5小時以下?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)如圖(1)所示,橢圓的中心在原點,焦點F1、F2在x軸上,A、B是橢圓的頂點,P是橢圓上一點,且PF1⊥x軸,PF2∥AB,求此橢圓的離心率;
(2)如圖(2)所示,雙曲線的一個焦點為F,虛軸的一個端點為B,如果直線FB與該雙曲線的一條漸近線垂直,求此雙曲線的離心率.


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】質檢部門對某工廠甲、乙兩個車間生產的![]() 個零件質量進行檢測.甲、乙兩個車間的零件質量(單位:克)分布的莖葉圖如圖所示.零件質量不超過
個零件質量進行檢測.甲、乙兩個車間的零件質量(單位:克)分布的莖葉圖如圖所示.零件質量不超過![]() 克的為合格.
克的為合格.
(1)質檢部門從甲車間![]() 個零件中隨機抽取
個零件中隨機抽取![]() 件進行檢測,若至少
件進行檢測,若至少![]() 件合格,檢測即可通過,若至少
件合格,檢測即可通過,若至少![]() 件合格,檢測即為良好,求甲車間在這次檢測通過的條件下,獲得檢測良好的概率;
件合格,檢測即為良好,求甲車間在這次檢測通過的條件下,獲得檢測良好的概率;
(2)若從甲、乙兩車間![]() 個零件中隨機抽取
個零件中隨機抽取![]() 個零件,用
個零件,用![]() 表示乙車間的零件個數,求
表示乙車間的零件個數,求![]() 的分布列與數學期望.
的分布列與數學期望.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com