
【題目】設函數![]() ,
,![]() ,其中
,其中![]() .若
.若![]() 恒成立,則當
恒成立,則當![]() 取得最小值時,
取得最小值時,![]() 的值為________.
的值為________.
【答案】![]()
【解析】
構造函數![]() ,可知函數
,可知函數![]() 的圖象關于點
的圖象關于點![]() 對稱,然后分
對稱,然后分![]() 三種情況進行討論,分析函數
三種情況進行討論,分析函數![]() 在區間
在區間![]() 上的單調性,得出函數
上的單調性,得出函數![]() 在區間
在區間![]() 上最值的可能取值,利用絕對值三角不等式可求出當
上最值的可能取值,利用絕對值三角不等式可求出當![]() 取得最小值時
取得最小值時![]() 的值.
的值.
令函數![]() ,則
,則![]() ,
,
因為![]() ,
,
所以函數![]() 的圖象關于點
的圖象關于點![]() 對稱,且
對稱,且![]() ,
,
所以當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增,
上單調遞增,
所以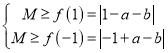 ,兩式相加可得,
,兩式相加可得,
![]() ,
,
此時,當![]() 時,
時,![]() 取得最小值
取得最小值![]() ;
;
當![]() 時,對任意的
時,對任意的![]() ,
,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞減,
上單調遞減,
所以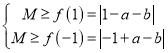 ,兩式相加可得,
,兩式相加可得,
![]() ,
,
此時當![]() 時,
時,![]() 取得最小值
取得最小值![]() ;
;
當![]() 時,令
時,令![]() ,得
,得![]() ,令
,令![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 極大值 |
| 極小值 |
|
不妨設![]() ,則
,則![]() ,則
,則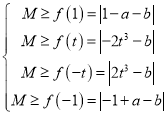 ,
,
所以![]() ,
,
因為![]() ,且
,且![]() ,所以
,所以![]() ,
,
因為![]() ,若
,若![]() ,則
,則![]() ,
,
若![]() ,則
,則![]() ,但
,但![]() ,
,
因為![]()
![]() ,
,
所以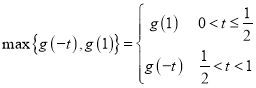 ,
,
當![]() 時,
時,![]() ,
,
當且僅當![]() 時,即當
時,即當![]() 時,
時,![]() 取得最小值
取得最小值![]() ;
;
當![]() 時,
時,![]() ,
,
綜上所述,當當![]() 時,
時,![]() 取得最小值
取得最小值![]() ,此時
,此時![]()
![]() .
.
故答案為:![]()


科目:高中數學 來源: 題型:
【題目】科赫曲線是一種外形像雪花的幾何曲線,一段科赫曲線可以通過下列操作步驟構造得到,任畫一條線段,然后把它均分成三等分,以中間一段為邊向外作正三角形,并把中間一段去掉,這樣,原來的一條線段就變成了4條小線段構成的折線,稱為“一次構造”;用同樣的方法把每條小線段重復上述步驟,得到16條更小的線段構成的折線,稱為“二次構造”,…,如此進行“![]() 次構造”,就可以得到一條科赫曲線.若要在構造過程中使得到的折線的長度達到初始線段的1000倍,則至少需要通過構造的次數是( ).(取
次構造”,就可以得到一條科赫曲線.若要在構造過程中使得到的折線的長度達到初始線段的1000倍,則至少需要通過構造的次數是( ).(取![]() ,
,![]() )
)

A.16B.17C.24D.25
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 經過點
經過點![]() ,且離心率為
,且離心率為![]() ,過其右焦點F的直線
,過其右焦點F的直線![]() 交橢圓C于M,N兩點,交y軸于E點.若
交橢圓C于M,N兩點,交y軸于E點.若![]() ,
,![]() .
.
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)試判斷![]() 是否是定值.若是定值,求出該定值;若不是定值,請說明理由.
是否是定值.若是定值,求出該定值;若不是定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
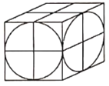
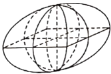
【題目】魏晉時期數學家劉徽在他的著作《九章算術注》中,稱一個正方體內兩個互相垂直的內切圓柱所圍成的幾何體為“牟合方蓋”(如圖所示),劉徽通過計算得知正方體的內切球的體積與“牟合方蓋”的體積之比應為![]() .若“牟合方蓋”的體積為
.若“牟合方蓋”的體積為![]() ,則正方體的外接球的表面積為__________.
,則正方體的外接球的表面積為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知極坐標系的極點為直角坐標系xOy的原點,極軸為x軸的正半軸,兩種坐標系中的長度單位相同,圓C的直角坐標方程為![]() ,直線l的參數方程為
,直線l的參數方程為![]() (t為參數),射線OM的極坐標方程為
(t為參數),射線OM的極坐標方程為![]() .
.
(1)求圓C和直線l的極坐標方程;
(2)已知射線OM與圓C的交點為O,P,與直線l的交點為Q,求線段PQ的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校在高二年級開設選修課,選課結束后,有6名同學要求改選歷史,現歷史選修課開有三個班,若每個班至多可再接收3名同學,那么不同的接收方案共有( )
A.150種B.360種C.510種D.512種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線l的參數方程為
中,直線l的參數方程為![]() (t為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]()
(1)求直線l的普通方程和曲線C的直角坐標方程;
(2)若直線l與曲線C相交于A,B兩點.求![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
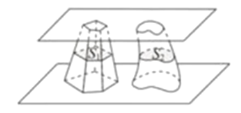
【題目】南北朝時代的偉大數學家祖暅在數學上有突出貢獻,他在實踐的基礎上提出祖暅原理:“冪勢既同,則積不容異”.其含義是:夾在兩個平行平面之間的兩個幾何體,被平行于這兩個平面的任意平面所截,如果截得的兩個截面的面積總相等,那么這兩個幾何體的體積相等,如圖,夾在兩個平行平面之間的兩個幾何體的體積分別為![]() ,被平行于這兩個平面的任意平面截得的兩個截面的面積分別為
,被平行于這兩個平面的任意平面截得的兩個截面的面積分別為![]() ,則“
,則“![]() 總相等”是“
總相等”是“![]() 相等”的( )
相等”的( )
A.充分不必要條件B.必要不充分條件
C.充分必要條件D.既不充分也不必要條件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com