
【題目】已知函數![]() .
.
(1)判斷函數![]() 的奇偶性,并給出證明;
的奇偶性,并給出證明;
(2)解不等式: ![]() ;
;
(3)若函數![]() 在
在![]() 上單調遞減,比較f(2)+f(4)+…+f(2n)與2n(n∈N*)的大小關系,并說明理由.
上單調遞減,比較f(2)+f(4)+…+f(2n)與2n(n∈N*)的大小關系,并說明理由.
【答案】(1)見解析;(2)原不等式的解集為:(-∞,1)∪(4,+∞);(3)見解析.
【解析】試題分析:(1)先求定義域,判斷關于原點是否對稱;再求![]() ,判斷與
,判斷與![]() 關系,最后根據奇偶性定義確定奇偶性(2)先根據定義確定函數單調性,再利用函數奇偶性以及單調性化簡不等式,最后解不等式x2+x+3<2x2-4x+7,可得解集(3)由函數
關系,最后根據奇偶性定義確定奇偶性(2)先根據定義確定函數單調性,再利用函數奇偶性以及單調性化簡不等式,最后解不等式x2+x+3<2x2-4x+7,可得解集(3)由函數![]() 在
在![]() 上單調遞減,得g(x)<g(1)=0,再作差化簡得f(2)+f(4)+…+f(2n)-2n=ln(2n+1)-2n=ln(2n+1)-[(2n+1)-1],最后根據單調性得結果
上單調遞減,得g(x)<g(1)=0,再作差化簡得f(2)+f(4)+…+f(2n)-2n=ln(2n+1)-2n=ln(2n+1)-[(2n+1)-1],最后根據單調性得結果
試題解析:(1)函數f(x)為奇函數.
證明如下:由![]() ,解得x<-1或x>1,
,解得x<-1或x>1,
所以函數的定義域為(-∞,-1)∪(1,+∞)對任意的x∈(-∞,-1)∪(1,+∞),
有![]() ,
,
所以函數f(x)為奇函數.
(2)任取x1,x2∈(1,+∞),且x1<x2,則![]() =
=![]() =
=![]() , 因為x2>x1>1,所以x1x2+x2-x1-1>x1x2-(x2-x1)-1>0,
, 因為x2>x1>1,所以x1x2+x2-x1-1>x1x2-(x2-x1)-1>0,
所以![]() ,所以f(x1)-f(x2)>0,
,所以f(x1)-f(x2)>0,
所以f(x1)>f(x2),所以函數y=f(x)在(1,+∞)單調遞減;
由f(x2+x+3)+f(-2x2+4x-7)>0得:f(x2+x+3)>-f(-2x2+4x-7),
即f(x2+x+3)>f(2x2-4x+7),
又![]() ,2x2-4x+7=2(x-1)2+5>1 ,
,2x2-4x+7=2(x-1)2+5>1 ,
所以x2+x+3<2x2-4x+7, 解得:x<1或x>4,
所以原不等式的解集為:(-∞,1)∪(4,+∞)
(3)f(2)+f(4)+…+f(2n)<2n(n∈N*).理由如下:
因為![]() ,
,
所以f(2)+f(4)+…+f(2n)-2n=ln(2n+1)-2n=ln(2n+1)-[(2n+1)-1],
又g(x)=lnx-(x-1)在(1,+∞)上單調遞減,
所以當x>1時,g(x)<g(1)=0,所以g(2n+1)<0,
即ln(2n+1)-[(2n+1)-1]<0,
故f(2)+f(4)+…+f(2n)<2n(n∈N


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中數學 來源: 題型:
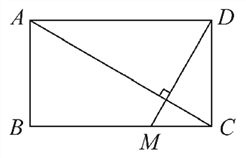
【題目】如圖所示,一個矩形花園里需要鋪兩條筆直的小路,已知矩形花園長AD=5m,寬AB=3m,其中一條小路定為AC,另一條小路過點D,問如何在BC上找到一點M,使得兩條小路AC與DM相互垂直?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保護學生的視力,教室內的日光燈在使用一段時間后必須更換.已知某校使用的100只日光燈在必須換掉前的使用天數如下表:
天數/天 | 151~180 | 181~210 | 211~240 | 241~270 | 271~300 | 301~330 | 331~360 | 361~390 |
燈管數/只 | 1 | 11 | 18 | 20 | 25 | 16 | 7 | 2 |
(1)試估計這種日光燈的平均使用壽命;
(2)若定期更換,可選擇多長時間統一更換合適?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新學年伊始,某中學學生社團開始招新,某高一新生對“海濟公益社”、“理科學社”、“高音低調樂社”很感興趣,假設她能被這三個社團接受的概率分別為 ![]() ,
, ![]() ,
, ![]() .
.
(1)求此新生被兩個社團接受的概率;
(2)設此新生最終參加的社團數為ξ,求ξ的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() =1(a>0)的焦點在x軸上,且橢圓C的焦距為2. (Ⅰ)求橢圓C的標準方程;
=1(a>0)的焦點在x軸上,且橢圓C的焦距為2. (Ⅰ)求橢圓C的標準方程;
(Ⅱ)過點R(4,0)的直線l與橢圓C交于兩點P,Q,過P作PN⊥x軸且與橢圓C交于另一點N,F為橢圓C的右焦點,求證:三點N,F,Q在同一條直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=lnx,g(x)=ax+ ![]() ,函數f(x)的圖象與x軸的交點也在函數g(x)的圖象上,且在此點有公切線. (Ⅰ)求a、b的值;
,函數f(x)的圖象與x軸的交點也在函數g(x)的圖象上,且在此點有公切線. (Ⅰ)求a、b的值;
(Ⅱ)試比較f(x)與g(x)的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,且
,且![]() ,向量
,向量![]() ,
, ![]() .
.
(1)求函數![]() 的解析式,并求當
的解析式,并求當![]() 時,
時, ![]() 的單調遞增區間;
的單調遞增區間;
(2)當![]() 時,
時, ![]() 的最大值為5,求
的最大值為5,求![]() 的值;
的值;
(3)當![]() 時,若不等式
時,若不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com