
【題目】已知函數![]()
(Ⅰ)討論函數![]() 在
在![]() 上的單調性;
上的單調性;
(Ⅱ)證明:![]() 恒成立.
恒成立.
【答案】(1),當![]() 時,
時,![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.(2)見解析
上單調遞減.(2)見解析
【解析】
(1)求出![]() (
(![]() ),通過當
),通過當![]() 時,當
時,當![]() 時,判斷導函數的符號,推出函數的單調區間即可.
時,判斷導函數的符號,推出函數的單調區間即可.
證法二:記函數![]() ,通過導數研究函數
,通過導數研究函數![]() 的性質,
的性質,![]() ,問題得證.
,問題得證.
(Ⅰ) ![]() (
(![]() ),
),
當![]() 時,
時,![]() 恒成立,所以,
恒成立,所以,![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,令
時,令![]() ,得到
,得到![]() ,所以,當
,所以,當![]() 時,
時,![]() ,
,![]() 單調遞增,當
單調遞增,當![]() 時,
時,![]() ,
,![]() 單調遞減.
單調遞減.
綜上所述,當![]() 時,
時,![]() 在
在![]() 上單調遞增;當
上單調遞增;當![]() 時,
時,![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(Ⅱ)證法一:由(Ⅰ)可知,當![]() 時,
時,![]() ,
,
特別地,取![]() ,有
,有![]() ,即
,即![]() ,所以
,所以![]() (當且僅當
(當且僅當![]() 時等號成立),
時等號成立),
因此,要證![]() 恒成立,只要證明
恒成立,只要證明![]() 在
在![]() 上恒成立即可,
上恒成立即可,
設![]() (
(![]() ),則
),則![]() ,
,
當![]() 時,
時,![]() ,
,![]() 單調遞減,當
單調遞減,當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
所以,當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上恒成立.
上恒成立.
因此,有![]() ,又因為兩個等號不能同時成立,所以有
,又因為兩個等號不能同時成立,所以有![]() 恒成立.
恒成立.
證法二:記函數![]() ,
,
則![]() ,可知
,可知![]() 在
在![]() 上單調遞增,又由
上單調遞增,又由![]() 知,
知, ![]() 在
在![]() 上有唯一實根
上有唯一實根![]() ,且
,且![]() ,則
,則![]() ,即
,即![]() (*),
(*),
當![]() 時,
時, ![]() 單調遞減;當
單調遞減;當![]() 時,
時, ![]() 單調遞增,
單調遞增,
所以![]() ,結合(*)式
,結合(*)式![]() ,知
,知![]() ,
,
所以![]() ,
,
則![]() ,即
,即![]() ,所以有
,所以有![]() 恒成立.
恒成立.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,側面
中,側面![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
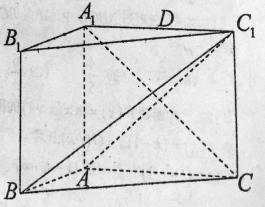
(1)求證:平面![]() 平面
平面![]() ;
;
(2)設![]() 是
是![]() 的中點,判斷并證明在線段
的中點,判斷并證明在線段![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 平面
平面![]() ,若存在,求點
,若存在,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AD⊥平面PCD,PD⊥CD,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2AB, ![]() 為棱PC上一點.
為棱PC上一點.

(Ⅰ)若點![]() 是PC的中點,證明:B
是PC的中點,證明:B![]() ∥平面PAD;
∥平面PAD;
(Ⅱ) ![]() 試確定
試確定![]() 的值使得二面角
的值使得二面角![]() -BD-P為60°.
-BD-P為60°.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場為吸引顧客消費推出一項優惠活動.活動規則如下:消費額每滿100元可轉動如圖所示的轉盤一次,并獲得相應金額的返券,假定指針等可能地停在任一位置.若指針停在A區域返券60元;停在B區域返券30元;停在C區域不返券.例如:消費218元,可轉動轉盤2次,所獲得的返券金額是兩次金額之和.

(1)若某位顧客消費128元,求返券金額不低于30元的概率;
(2)若某位顧客恰好消費280元,并按規則參與了活動,他獲得返券的金額記為![]() (元).求隨機變量
(元).求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司生產一種電子儀器的固定成本為20000元,每生產一臺儀器需增加投入100元,已知總收益滿足函數:  ,其中
,其中![]() 是儀器的月產量.(注:總收益=總成本+利潤)
是儀器的月產量.(注:總收益=總成本+利潤)
(1)將利潤![]() 表示為月產量
表示為月產量![]() 的函數;
的函數;
(2)當月產量為何值時,公司所獲利潤最大?最大利潤為多少元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】針對時下的“抖音熱”,某校團委對“學生性別和喜歡抖音是否有關”作了一次調查,其中被調查的女生人數是男生人數的![]() ,男生喜歡抖音的人數占男生人數的
,男生喜歡抖音的人數占男生人數的![]() ,女生喜歡抖音的人數占女生人數
,女生喜歡抖音的人數占女生人數![]() 若有95%的把握認為是否喜歡抖音和性別有關,則男生至少有( )人.
若有95%的把握認為是否喜歡抖音和性別有關,則男生至少有( )人.
(K2≥k0) | 0.050 | 0.010 |
k0 | 3.841 | 6.635 |
A. 12B. 6C. 10D. 18
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com