【題目】“黃梅時節家家雨”“梅雨如煙暝村樹”“梅雨暫收斜照明”
江南梅雨的點點滴滴都流潤著濃洌的詩情
每年六、七月份，我國長江中下游地區進入持續25天左右的梅雨季節，如圖是江南Q鎮
年梅雨季節的降雨量
單位：
的頻率分布直方圖，試用樣本頻率估計總體概率，解答下列問題：
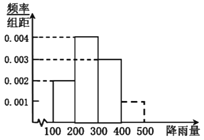
Ⅰ
“梅實初黃暮雨深”假設每年的梅雨天氣相互獨立，求Q鎮未來三年里至少有兩年梅雨季節的降雨量超過350mm的概率；
Ⅱ“江南梅雨無限愁”在Q鎮承包了20畝土地種植楊梅的老李也在犯愁，他過去種植的甲品種楊梅，平均每年的總利潤為28萬元而乙品種楊梅的畝產量
畝與降雨量之間的關系如下面統計表所示，又知乙品種楊梅的單位利潤為
元
，請你幫助老李排解憂愁，他來年應該種植哪個品種的楊梅可以使總利潤
萬元的期望更大？需說明理由
降雨量 |
|
|
|
|
畝產量 | 500 | 700 | 600 | 400 |
【答案】
乙
【解析】
由頻率分布直方圖可求出降雨量超過
的概率，利用獨立重復試驗的概率公式計算三年里至少有兩年梅雨季節的降雨量超過的概率.
根據題意，列出隨機變量
（萬元）的分布列并求期望，與甲品種的平均值作比較得出結論.
頻率分布直方圖中第四組的頻率為
.
江南
地區在梅雨季節時降雨量超過的概率為
.
所以地區未來三年里至少有兩年梅雨季節的降雨量超過的概率為
（或0.15625）.
根據題意，總利潤為
（元），其中
.
所以隨機變量（萬元）的分布列如下表.
| 27 | 35 | 31.2 | 22.4 |
| 0.2 | 0.4 | 0.3 | 0.1 |
故總利潤（萬元）的數學期望
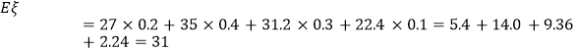（萬元）.
因為31>28，所以老李來年應該種植乙品種楊梅，可使總利潤的期望更大.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】設f（x）是定義在實數集R上的函數，且y=f（x+1）是偶函數，當x≥1時，f（x）=2x﹣1，則f（
），f（
），f（
）的大小關系是（ ）
A. f（）＜f（）＜f（） B. f（）＜f（）＜f（）
C. f（）＜f（）＜f（） D. f（）＜f（）＜f（）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C：
（a＞b＞0）的兩個焦點分別為F1，F2，離心率為
，過F1的直線l與橢圓C交于M，N兩點，且△MNF2的周長為8．
（1）求橢圓C的方程；
（2）若直線y＝kx＋b與橢圓C分別交于A，B兩點，且OA⊥OB，試問點O到直線AB的距離是否為定值，證明你的結論．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列說法:①方程
表示的圖形是一個點;②命題“若
，則
或
”為真命題;③已知雙曲線
的左右焦點分別為
，
，過右焦點被雙曲線截得的弦長為4的直線有3條;④已知橢圓
上有兩點
，
，若點
是橢圓
上任意一點，且
，直線
，
的斜率分別為
，
，則
為定值
.
其中說法正確的序號是________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線
，
.
(1)若直線
，
分別經過定點
，
，求定點，的坐標;
(2)是否存在一個定點
，使得與的交點到定點的距離為定值?如果存在，求出定點的坐標及定值
;如果不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，某小區準備將閑置的一直角三角形地塊開發成公共綠地，圖中
.設計時要求綠地部分（如圖中陰影部分所示）有公共綠地走道
，且兩邊是兩個關于走道對稱的三角形（
和
）.現考慮方便和綠地最大化原則，要求點
與點
均不重合，
落在邊
上且不與端點
重合，設
.
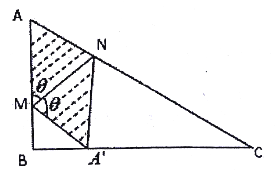
（1）若
，求此時公共綠地的面積；
（2）為方便小區居民的行走，設計時要求
的長度最短，求此時綠地公共走道的長度.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】盡管目前人類還無法準確預報地震,但科學家通過研究,已經對地震有所了解,例如，地震釋放出的能量
(單位:焦耳)與地震里氏震級
之間的關系為
.
(1)已知地震等級劃分為里氏
級,根據等級范圍又分為三種類型,其中小于
級的為“小地震”,介于級到
級之間的為“有感地震”,大于級的為“破壞性地震”若某次地震釋放能量約
焦耳，試確定該次地震的類型;
(2)2008年汶川地震為里氏
級,2011年日本地震為里氏
級,問:2011年日本地震所釋放的能量是2008年汶川地震所釋放的能量的多少倍? (取
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
