【題目】已知△ABC的內角A，B，C所對的邊分別為a，b，c，且滿足 
= 
． （Ⅰ）求C的值；
（Ⅱ）若 
=2，b=4 
，求△ABC的面積．
【答案】解：（Ⅰ）∵ 
= 
． ∴ = 
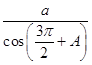，由正弦定理可得： 
，可得：tanC= 
，
∴C= 
．
（Ⅱ）∵C= ， 
=2，b=4 
，
∴由余弦定理c2=a2+b2﹣2abcosC，可得：（2a）2=a2+（4 ）2﹣2× 
，
整理可得：a2+4a﹣16=0，解得：a=2 
﹣2，
∴S△ABC= 
absinC= 
（2 ﹣2）× 
× =2 
﹣2
【解析】（Ⅰ）利用誘導公式，正弦定理，同角三角函數基本關系式化簡已知等式可得tanC= 
，利用特殊角的三角函數值即可得解C的值．（Ⅱ）由余弦定理可求a的值，進而利用三角形面積公式即可計算得解．
【考點精析】解答此題的關鍵在于理解正弦定理的定義的相關知識，掌握正弦定理:
，以及對余弦定理的定義的理解，了解余弦定理:
;
;
．
科目：高中數學 來源： 題型：
【題目】圖中的程序框圖的算法思路來源于我國古代數學名著《九章算術》中的“更相減損術”．執行該程序框圖，若輸入的a，b，i的值分別為8，10，0，則輸出的a和i和值分別為（ ） 
A.2，5
B.2，4
C.0，4
D.0，5
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了得到函數 
的圖象，只需把y=3sin2x上的所有的點（ ）
A.向左平行移動 
長度單位
B.向右平行移動 長度單位
C.向右平行移動 
長度單位
D.向左平行移動 長度單位
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】平面內到定點F（0，1）和定直線l：y=﹣1的距離之和等于4的動點的軌跡為曲線C，關于曲線C的幾何性質，給出下列四個結論： ①曲線C的方程為x2=4y；
②曲線C關于y軸對稱
③若點P（x，y）在曲線C上，則|y|≤2；
④若點P在曲線C上，則1≤|PF|≤4
其中，所有正確結論的序號是 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】函數y=log 
cos（ 
﹣2x）的遞增區間是 （ ）
A.[﹣ 
+kπ， +kπ]（k∈Z）
B.[﹣ +kπ，kπ）（k∈Z）
C.[ +kπ， 
+kπ]（k∈Z）
D.[ +kπ， +kπ）（k∈Z）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=Asin（ωx+φ）（A，ω＞0，0＜|φ|＜π）在一個周期內的圖象如圖所示．
（1）求函數f（x）的解析式；
（2）求g（x）=f（3x+
）﹣1在[﹣
， 
]上的值域．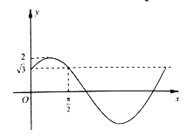
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
