設函數f(x)=x(x-1)(x-a),(a>1)
(1)求導數f′(x)并證明f(x)有兩個不同的極值點x1,x2;
(2)若不等式f(x1)+f(x2)≤0成立,求a的取值范圍.
【答案】
分析:(1)利用求導法則求出f(x)的導函數,令f'(x)=0考慮到判別式大于零得到兩個極值點,設x
1<x
2,討論函數的增減性得到x
1是極大值點,x
2是極小值點;
(2)把x
1,x
2代入到f(x)中求出函數值代入不等式f(x
1)+f(x
2)≤0中,在利用根與系數的關系化簡得到關于a的不等式,求出解集即可.
解答:解:(1)f'(x)=3x
2-2(1+a)x+a.
令f'(x)=0得方程
3x
2-2(1+a)x+a=0.
因△=4(a
2-a+1)≥4a>0,故方程有兩個不同實根x
1,x
2不妨設x
1<x
2,由f'(x)=3(x-x
1)(x-x
2)可判斷f'(x)的符號如下:
當x<x
1時,f'(x)>0;
當x
1<x<x
2時,f'(x)<0;
當x>x
2時,f'(x)>0
因此x
1是極大值點,x
2是極小值點.
(2)因f(x
1)+f(x
2)≤0,故得不等式x
13+x
23-(1+a)(x
12+x
22)+a(x
1+x
2)≤0.
即(x
1+x
2)[(x
1+x
2)
2-3x
1x
2]-(1+a)[(x
1+x
2)
2-2x
1x
2]+a(x
1+x
2)≤0.
又由(I)知
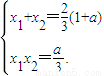
代入前面不等式,兩邊除以(1+a),并化簡得
2a
2-5a+2≥0.
解不等式得a≥2或a≤

(舍去)
因此,當a≥2時,不等式f(x
1)+f(x
2)≤0成立.
點評:考查學生求導數及利用導數研究函數極值的能力,靈活運用一元二次方程根與系數的關系解決數學問題的能力.

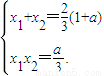
 (舍去)
(舍去)

 閱讀快車系列答案
閱讀快車系列答案